Question
1) Find the invariants of the matrix
0 1 0
0 0 0
0 0 0 of a linear transformation T in A(v) ?
2) Find the companion matrix of the polynomial ( x+1)2 ?
3) show that two real symmetric matrices are congruent if and only if they have the same rank and signature?
rank(A) = 1
det(A) = 0
trace(A) = 0
The matrix is not symmetric.
characteristic polynomial of the given matrix is x3
companion matrix of the polynomial (x+1)2
0 1
-1 -2
A real symmetric matrix of rank r is congruent over the field of real numbers to a canonical matrix
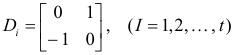
The integer p is called the index of the matrix and s = p - (r - p) is called the signature.
The index of a symmetric or Hermitian matrix is the number of positive elements when it is transformed to a diagonal matrix. The signature is the number of positive terms diminished by the number of negative terms and the total number of nonzero terms is the rank.
now solve it
