45 - Algebra Questions Answers

Mathematics >> Algebra >> Sequence and Series IIT JEE

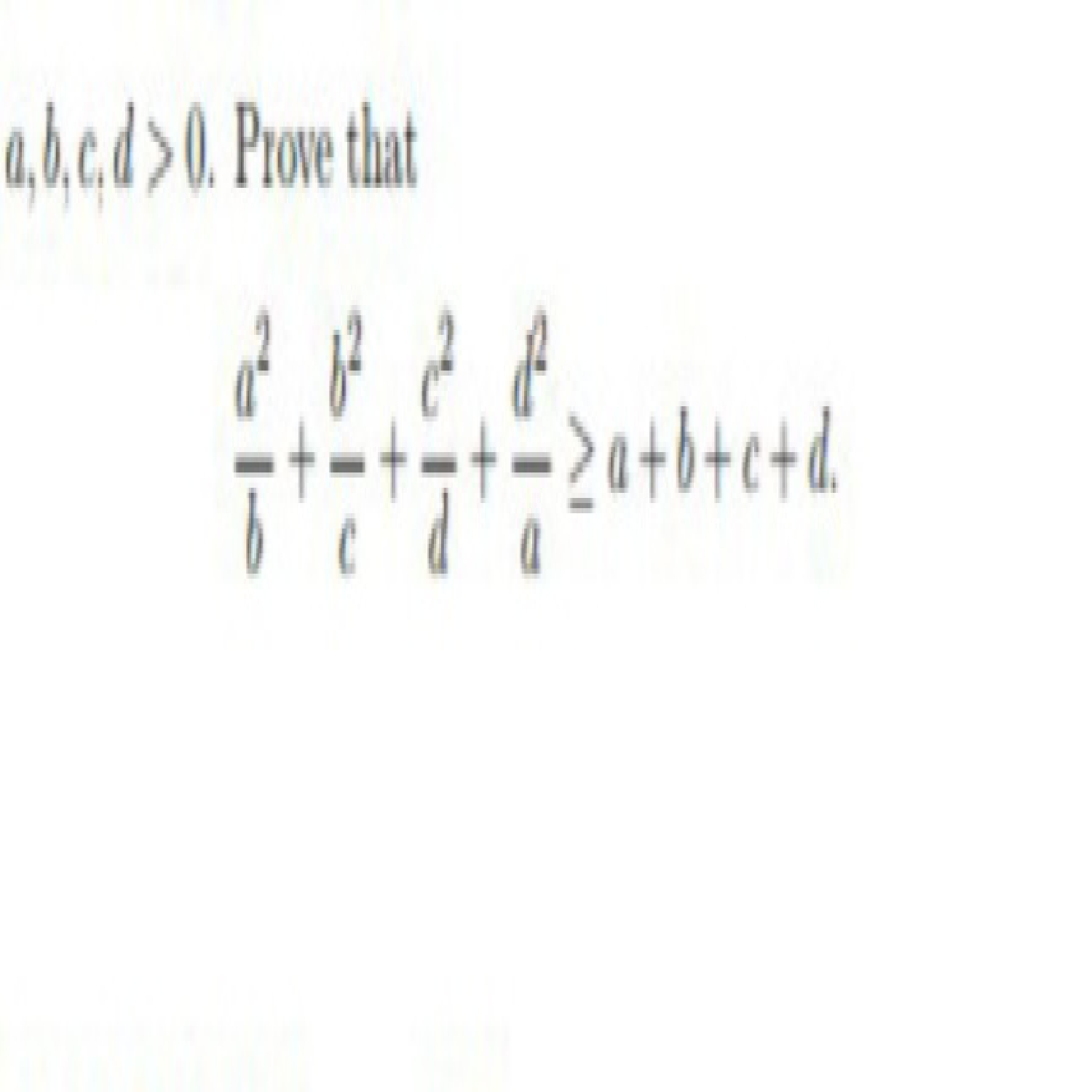
Find Sum to n terms

x/1-x² + x²/1-x⁴ + x⁴/1-x⁸ + ....

Asked By: LUFFY

is this question helpfull: 3 0 submit your answer

Joshi sir comment

$\frac{x}{1 - x^{2}} = \frac{1}{1 - x} - \frac{1}{1 - x^{2}} b r e a k a l l t e r m s s i m i l a r l y a n d s o l v e$

Maths >> Algebra >> Equation and Enequalities IIT JEE

No. of integral roots of the eqn. x⁸ - 24 x⁷ - 18x⁵ + 39 x² + 1155 = 0 .

Asked By: VAIBHAV GUPTA

is this question helpfull: 18 3 submit your answer

Joshi sir comment

two times sign change so 2 positive roots

Maths >> Algebra >> Equation and Enequalities IIT JEE

let a,b,c be three distinct real numbers such that each of expression ax²+bx+c,bx²+cx+a,cx²+ax+b are positive for all x ε R and let

α=bc+ca+ab/a²+b²+c² then

(A) α<4 (B) α<1 (C) α>1/4 (D) α>1

THIS IS MULTIPLE CHOICE QUESTION

Asked By: AKASH

is this question helpfull: 7 0 read solutions ( 1 ) | submit your answer

Joshi sir comment

if ax²+bx+c is positive for real x

then b²< 4ac similarly others

on adding all inequalities we get b² + c² + a²< 4(ac+ab+bc)

now get answer

Maths >> Algebra >> Binomial Theorem Engineering Exam

Find sum of series..1*(n)²+ 2*(n-1)²+3*(n-2)² +...+n .

Asked By: RESHU SINGH

is this question helpfull: 10 3 submit your answer

Joshi sir comment

general term of the series = r(n+1-r)²= r(n+1)² + r³ - 2(n+1)r²

now put sigma then solve

Maths >> Algebra >> Binomial Theorem IIT JEE

If x+y = 1 ,then ∑ r ⁿC_rx^ry^n-requals nx....How??

Asked By: RESHU SINGH

is this question helpfull: 6 1 submit your answer

Joshi sir comment

∑ r ⁿC_rx^ry^n-r

= ∑ r ⁿC_rx^r(1-x)^n-r

= ∑ r n!/r!(n-r)! x^r(1-x)^n-r

= n (n-1)!/(r-1)!(n-r)! x^r(1-x)^n-r

= n ⁽^n-1)C₍_r-1)x^r(1-x)^n-r

= n ⁽^n-1)C_rx^r+1(1-x)^n-r-1let r = r+1

= nx ⁽^n-1)C_rx^r(1-x)^n-r-1

^{now solve}

Maths >> Algebra >> Binomial Theorem Others

What is the value of 0⁄0? if its otherthan 1, then how this can be true: lim (e^x-1)/x = 1

^{x −−>0}

Asked By: BONEY HAVELIWALA

is this question helpfull: 2 1 submit your answer

Joshi sir comment

exact 0 and lim tends to 0 are different

Maths >> Algebra >> Permutation and Combination IIT JEE

what will be the rank of word OPTION in the dictionary of words formed by letters of the word OPTION

Asked By: JIGYASA KUMAR

is this question helpfull: 13 6 submit your answer

Joshi sir comment

OPTION

ordered way INOOPT

total words = 6!/2! = 360

so rank = (360/6)*2+([60*2]/5)*3+(24/4)*3+(6/3)*0+(2/2)*1+1 = 120+72+18+0+1+1 = 212

Maths >> Algebra >> Matrices and Determinant Engineering Exam

prove using property of determinant

1. a+b+c -c -b

-c a+b+c -a = 2(a+b)( b+c ) (c+a)

-b -a a+b+c

Asked By: SONAM SHARMA

is this question helpfull: 12 4 submit your answer

Joshi sir comment

first use C1 = C1+C2+C3

then R1 = R1+R2 and R2 = R2+R3

after it solve mathematically

Maths >> Algebra >> Permutation and Combination IIT JEE

rank of the number 3241?(digits cannot be repeated)

Asked By: HARSHITH

is this question helpfull: 7 2 read solutions ( 1 ) | submit your answer

Joshi sir comment

total numbers = 4*3*2*1 = 24

on arranging these numbers in order we get 1234

so rank = [24/4]*2+[6/3]*1+[2/2]*1+1 = 16

Maths >> Algebra >> Matrices and Determinant Engineering Exam

which is the 4 digit number whose second digit is thrice the first digit and 3'rd digit is sum of 1'st and 2'nd and last digit is twice the second digit.

Asked By: SAURABH TIWARI

is this question helpfull: 6 2 read solutions ( 2 ) | submit your answer

Joshi sir comment

let the 4 digit number is 1000a+100b+10c+d

then according to the given condition b=3a, c=a+b, d=2b

so c=4a, d=6a and b=3a

on putting all the values we get number = 1000a+100(3a)+10(4a)+6a = 1346a

on putting a =1, number = 1346

45 - Algebra Questions Answers

which is the 4 digit number whose second digit is thrice the first digit and 3'rd digit is sum of 1'st and 2'nd and last digit is twice the second digit.

Login Here

Forget Password

Registration Form