5 - Applications of differentiation Questions Answers

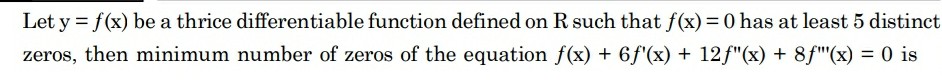
$$\begin{gathered} The general solution of this kind of \\ differential eq. is y = e^{ax} \\ Let a function g\left(x\right) = e^{ax}f\left(x\right) \left(1\right) \\ differentiate eq. \left(1\right) thrice for getting g^{,,,}\left(x\right) \\ now for getting the same function as given \\ find a. you get the same function for \\ a = 1/2. clearly, for min 5 zeros of g\left(x\right), \\ there are min 2 zeros for g^{,,,}\left(x\right). \\ solve and inform if face any problem. \end{gathered}$$

perimeter = 4 so 2Y + X + πX/2 = 4

and area = XY + [π(X/2)²]/2

put Y from 1st equation to 2nd we get A = X[4-X{1+(π/2)}]/2 + πX²/8

now calculate dA/dX and then compare it to zero

X will be 8/(4+π)

f(x) is monotonically increasing so f '(x)>0 and f '' (x) >0 implies that increment of function increases rapidly with increase in x 

These informations provide the following informations about the nature of inverse of f(x) 

1) f ^-1 (x) will also be an increasing function but its rate of increase decreases with increasing x

2) for x₁ < x₂ < x₃ ,  å{f ^-1(x_i)/3} < f ^-1({x₁+x₂+x₃}/3), 

The same result for f(x) will be 

  å{f (x_i)/3} > f ({x₁+x₂+x₃}/3), 

f(x+y) = f(x) + f(y) + 2xy - 1 

so f(0) = 1      obtain this by putting x = 0 and y = 0

now f ^' (x+y) = f ^' (x)  + 2y         on differentiating with respect to x

take x = 0, we get f ^' (y) = f ^'(0) + 2y

or f ' (x) = cosα + 2x

now integrate this equation within the limits 0 to x

we get f(x) = x² + cosα x + 1

its descreminant is negative and coefficient of x² is positive so f(x) > 0