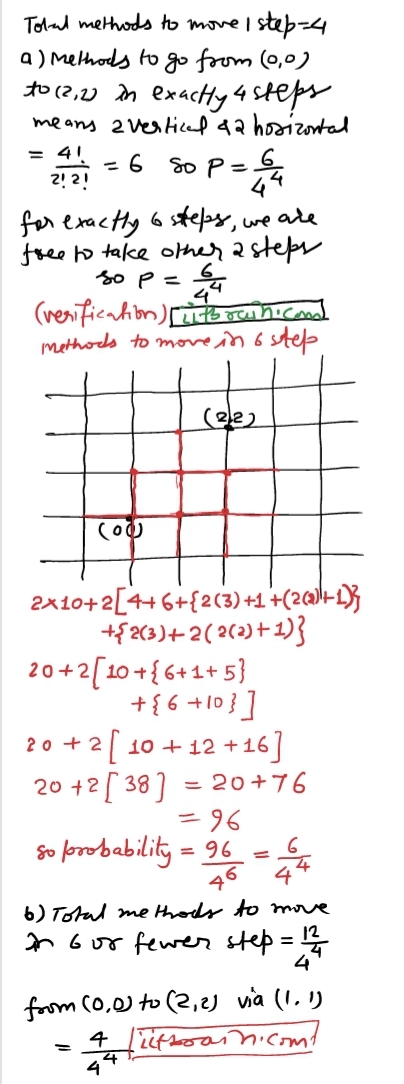
4 - Probability Questions Answers

Mathematics >> Algebra >> Probability IIT JEE

Sir please help in this question i got stuck in p&c part.

Asked By: UTKARSH MAURYA

is this question helpfull: 1 1 submit your answer

Joshi sir comment

Mathematics >> Algebra >> Probability IIT JEE

There are 8 distinct boxes and each box can hold any number of balls. A child having 4 identical balls randomly choose four boxes. Then another child having four balls, identical to the previous mentioned, again puts one ball in each of the arbitrary chosen four boxes. The probability that there are balls in at least 6 boxes is

Sir pls solve

Asked By: KANDUKURI ASHISH

is this question helpfull: 1 0 submit your answer

Joshi sir comment

Mathematics >> Algebra >> Probability IIT JEE

Is there a way to do this in terms of area in a coordinate plane. Where difference of larger and smaller can be difference in x coordinate for 1st player and difference in y coordinate for 2nd player

Asked By: LUFFY

is this question helpfull: 0 0 submit your answer

Joshi sir comment

$P r o b a b i l i t y t o g e t f o l l o w i n g d i f f e r e n c e s d i f f e r e n c e p r o b a b i l i t y 0 6 / 36 1 10 / 36 2 8 / 36 3 6 / 36 4 4 / 36 5 2 / 36 S o r e q u i r e d p r o b a b i l i t y = 1 - 2 [\frac{6}{36} (\frac{4}{36} + \frac{2}{36}) + \frac{10}{36} (\frac{2}{36})] n o w s o l v e p r o b l e m i s b a s e d o n i n t e g r a l v a l u e s s o a r e a i s n o t v e r y u s e f u l$

Maths >> Algebra >> Probability IIT JEE

A housewife buys a dozen eggs of which two turn out to be bad. She chooses four eggs for breakfast. Find thd chance that she chooses (1) all good eggs (2)three good and one bad (3)two good and two bad (4)at least one bad egg.

Asked By: SAHDEV SINGH

is this question helpfull: 6 0 read solutions ( 1 ) | submit your answer

Joshi sir comment

1) (10/12)(9/11)(8/10)(7/9)

2) 4(10/12)(9/11)(8/10)(2/9)

3) (4*3/2)(10/12)(9/11)(2/10)(1/9)

4) 1 - (10/12)(9/11)(8/10)(7/9)

Login Here

Registration Form

Your Full Name :

Your Email Address :

Country :

State :

4 - Probability Questions Answers

Login Here

Forget Password

Registration Form