12 - Limit Continuity and Differentiability Questions Answers

Mathematics >> Calculus >> Limit Continuity and Differentiability IIT JEE

Asked By: RISHABH SHUKLA

is this question helpfull: 0 0 read solutions ( 1 ) | submit your answer

Joshi sir comment

Mathematics >> Calculus >> Limit Continuity and Differentiability IIT JEE

Asked By: HARDIK

is this question helpfull: 0 0 submit your answer

Joshi sir comment

Mathematics >> Calculus >> Limit Continuity and Differentiability IIT JEE

Find

lim n→∞ ⁿ√(n!) / n

Asked By: LUFFY

is this question helpfull: 1 0 submit your answer

Joshi sir comment

Maths >> Calculus >> Limit Continuity and Differentiability IIT JEE

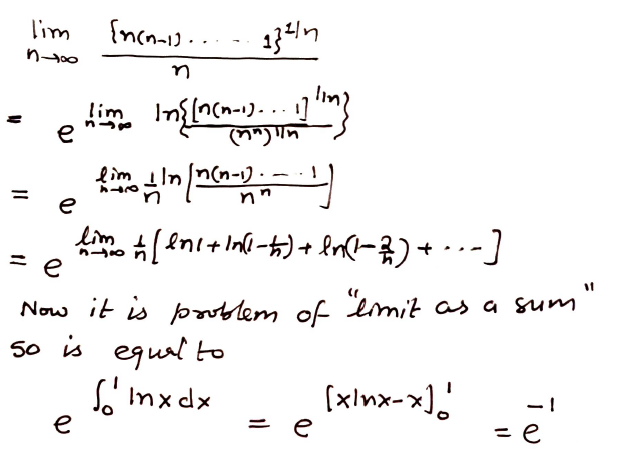
Sir , i have solved limx-->0 (sin^-1x - tan^-1x )/x³. plz have a look on others.

Asked By: VISHAL PHOGAT

is this question helpfull: 6 2 submit your answer

Joshi sir comment

limx-->0 (sin^-1x - tan^-1x )/x³

use D L Hospital rule or expansion of sin^-1x and tan^-1x to solve it

Maths >> Calculus >> Limit Continuity and Differentiability IIT JEE

no of solutions of e^{-x^2/2} - x²= 0 are

Asked By: VISHAL PHOGAT

is this question helpfull: 5 0 submit your answer

Joshi sir comment

two intersecting points means two solutions

Maths >> Calculus >> Limit Continuity and Differentiability Engineering Exam

lim x»infinity( ((x+1)(x+2)(x+3)(x+4))^¼ - x )

Asked By: VISHAL PHOGAT

is this question helpfull: 4 0 submit your answer

Joshi sir comment

multiply with the conjugate in numerator again and again you will get

lim_x->∞ ((x+1)(x+2)(x+3)(x+4) - x⁴)/((x+1)(x+2)(x+3)(x+4))^1/4 + x )*((x+1)(x+2)(x+3)(x+4))^1/2 + x² )

after solving the numerator get a 3 power expression of x then take 3 power of x common, similarly take x and 2 power of x from the first and second denominator terms

Maths >> Calculus >> Limit Continuity and Differentiability IIT JEE

lim n--> ∞ 4^n/n!

Asked By: HIMANSHU MITTAL

is this question helpfull: 3 1 submit your answer

Joshi sir comment

limn->∞ 4ⁿ/ n!

= lim_n->∞ [4/1][4/2][4/3][4/4][4/5][4/6][4/7]................................[4/n]

besides first four bracket, all brackets are real numbers less than 1 so their product will be zero for n tends to infinite

Maths >> Calculus >> Limit Continuity and Differentiability Others

Importance High!!!!!!!!!!!!!!!!!

Dear Sir / Madam

Myself Rajeev Shrivastava, I am putting a signs series in front of you which based on numbers from 01 to 100. Actually I want to know that what reason of behind Approx equability of signs is

(++), (+-), (--) & (-+) at end of the month or year between the below mentioned.

Let's define a kind of mapping:
0↔1
2↔3
4↔5
6↔7
8↔9

(+) means: an Even number
(-) means: an Odd number

I simply say: for any EO (+-) it exists an OE (-+) which is paired to.
And that's true since each E is mapped to a O and vice versa (1 to 1 relation where "f(f(x))=x" ) !
E.g.: 29 ↔ 83

There is 25 numbers in the EO (+-) group, so 25 in OE (+-).
There is 25 numbers in the EE (++) group, so 25 in OO (--).

Picking a number at random between 01 and 100 inclusive is choosing equitably in EO, OE, EE or OO group. (25% for each)

So, I really need of your help to solve a puzzle please. I just am trying to make you understand what type of solution I need:

There are some results for your review:

MONTH	DATE	DAY	FIRST_SERIES		SECOND_SERIES		FIRST_SERIES	SECOND_SERIES
APR	1	SUN	+	-	-	+	+-	-+
APR	2	MON	+	+	-	+	++	-+
APR	3	TUE	+	-	+	-	+-	+-
APR	4	WED	+	+	+	+	++	++
APR	5	THU	-	+	-	+	-+	-+
APR	6	FRI	+	+	+	-	++	+-
APR	7	SAT	+	-	-	+	+-	-+
APR	8	SUN	-	+	+	-	-+	+-
APR	9	MON	-	+	-	+	-+	-+
APR	10	TUE	+	+	+	+	++	++
APR	11	WED	+	+	-	-	++	--
APR	12	THU	-	+	-	-	-+	--
APR	13	FRI	+	+	+	+	++	++
APR	14	SAT	+	-	+	-	+-	+-
APR	15	SUN	+	-	+	-	+-	+-
APR	16	MON	-	-	+	+	--	++
APR	17	TUE	-	-	+	+	--	++
APR	18	WED
APR	19	THU
APR	20	FRI
APR	21	SAT
APR	22
APR	23

(Complete sheets for the year 2011 and 2012 are attached with this mail)

You can see that there are two times falls in a day of pair make by even (+) and odd (-) signs, i.e. (++), (+-), (--) & (-+) as above said.

The total of pair combination signs become approx equal to each other at the end of the month or year (every year- so, I am sending you attachment to go through the year’s result).

By this analysis:

1- I want to know that what is the relation between current falling signs and past fell signs.

2- How can I come to know, what type of combination of sign would be any particular date or day.

3- As you can seen on 22^nd and 23^rd April’2012 I don’t know what combination of sign is.

4- There is surety that there is some relation between current First fall of combination of signs and past fall or First fall of combination of signs and Second fall of combination of signs.

Please help me to how come to know what type of fall may be for next day by reviewing past or first combination of signs. So reply or elaborate me with an example.

I would be very grateful to you till entire life.

Regards

RAJEEV SHRIVASTAVA

Importance High!!!!!!!!!!!!!!!!!

Dear Sir / Madam

Myself Rajeev Shrivastava, I am putting a signs series in front of you which based on numbers from 01 to 100. Actually I want to know that what reason of behind Approx equability of signs is

(++), (+-), (--) & (-+) at end of the month or year between the below mentioned.

Let's define a kind of mapping:
0↔1
2↔3
4↔5
6↔7
8↔9

(+) means: an Even number
(-) means: an Odd number

I simply say: for any EO (+-) it exists an OE (-+) which is paired to.
And that's true since each E is mapped to a O and vice versa (1 to 1 relation where "f(f(x))=x" ) !
E.g.: 29 ↔ 83

There is 25 numbers in the EO (+-) group, so 25 in OE (+-).
There is 25 numbers in the EE (++) group, so 25 in OO (--).

Picking a number at random between 01 and 100 inclusive is choosing equitably in EO, OE, EE or OO group. (25% for each)

So, I really need of your help to solve a puzzle please. I just am trying to make you understand what type of solution I need:

There are some results for your review:

MONTH	DATE	DAY	FIRST_SERIES		SECOND_SERIES		FIRST_SERIES	SECOND_SERIES
APR	1	SUN	+	-	-	+	+-	-+
APR	2	MON	+	+	-	+	++	-+
APR	3	TUE	+	-	+	-	+-	+-
APR	4	WED	+	+	+	+	++	++
APR	5	THU	-	+	-	+	-+	-+
APR	6	FRI	+	+	+	-	++	+-
APR	7	SAT	+	-	-	+	+-	-+
APR	8	SUN	-	+	+	-	-+	+-
APR	9	MON	-	+	-	+	-+	-+
APR	10	TUE	+	+	+	+	++	++
APR	11	WED	+	+	-	-	++	--
APR	12	THU	-	+	-	-	-+	--
APR	13	FRI	+	+	+	+	++	++
APR	14	SAT	+	-	+	-	+-	+-
APR	15	SUN	+	-	+	-	+-	+-
APR	16	MON	-	-	+	+	--	++
APR	17	TUE	-	-	+	+	--	++
APR	18	WED
APR	19	THU
APR	20	FRI
APR	21	SAT
APR	22
APR	23

(Complete sheets for the year 2011 and 2012 are attached with this mail)

You can see that there are two times falls in a day of pair make by even (+) and odd (-) signs, i.e. (++), (+-), (--) & (-+) as above said.

The total of pair combination signs become approx equal to each other at the end of the month or year (every year- so, I am sending you attachment to go through the year’s result).

By this analysis:

1- I want to know that what is the relation between current falling signs and past fell signs.

2- How can I come to know, what type of combination of sign would be any particular date or day.

3- As you can seen on 22^nd and 23^rd April’2012 I don’t know what combination of sign is.

4- There is surety that there is some relation between current First fall of combination of signs and past fall or First fall of combination of signs and Second fall of combination of signs.

Please help me to how come to know what type of fall may be for next day by reviewing past or first combination of signs. So reply or elaborate me with an example.

I would be very grateful to you till entire life.

Regards

RAJEEV SHRIVASTAVA

Asked By: RAJEEV SHRIVASTAVA

is this question helpfull: 8 1 read solutions ( 1 ) | submit your answer

Joshi sir comment

If you are making the sequence on the basis of dates then you should take signs accordingly then you can make this sequence for many years

for example if you take 23 june then first sign series will be +-, + for even number and - for odd number , now as conversion rule as you gave in your explanation 23 will be converted to 32 so second series will be -+

similarly you can make it for any date

for example 29 december first series will be +- and its conversion is 38 so next series will be -+

if you are thinking something else then explain your question correctly

Maths >> Calculus >> Limit Continuity and Differentiability IIT JEE

ABC is an isosceles triangle inscribed in a circle of radius r. If AB=AC and h is the altitude from A to BC. and P and φ denote the perimeter and area of the triangle respectively, then lim n−» 0 φ/p³ is equal to??

Asked By: AMIT DAS

is this question helpfull: 8 0 submit your answer

Joshi sir comment

first draw a cirle and triange inside it , consider angle B and angle C asα so angle A = 180-2α, let centre of the circle is O and D is the point in the line BC where altitude meets in the line BC, given that altitude = h and radius = r

so AB = AC = h cosecα and BC = 2 h cotα so

p = 2 h (cosecα + cotα)

and φ = 1/2 2 h cotα h = h² cotαa

and in triangle OBD angle OBD = 2α - 90 so cos(2α - 90) = h cotα /r implies that h = 2 r sin²α

now i think limit will be based on h not n

lim _{h−» 0} φ/p³ = 1/128r

for getting solution put p and φ first then put h in terms of r, you will get an equation based on α and r,

convert lim_h->0 to limα->0 because when h will be 0, α will also be 0

Maths >> Calculus >> Limit Continuity and Differentiability IIT JEE

limit n tends to ∞

then

(x^n)/(n!) equals

Asked By: AMIT DAS

is this question helpfull: 5 0 submit your answer

Joshi sir comment

let y = lim n->∞ (xⁿ/n!)

or y = x lim n->∞ (1/n) lim n->∞ x^n-1/(n-1)!

or y = 0

12 - Limit Continuity and Differentiability Questions Answers

Login Here

Forget Password

Registration Form