11 - Equations and Inequalities Questions Answers
Solve in integers the equation
If a,b and c are positive real numbers, show that
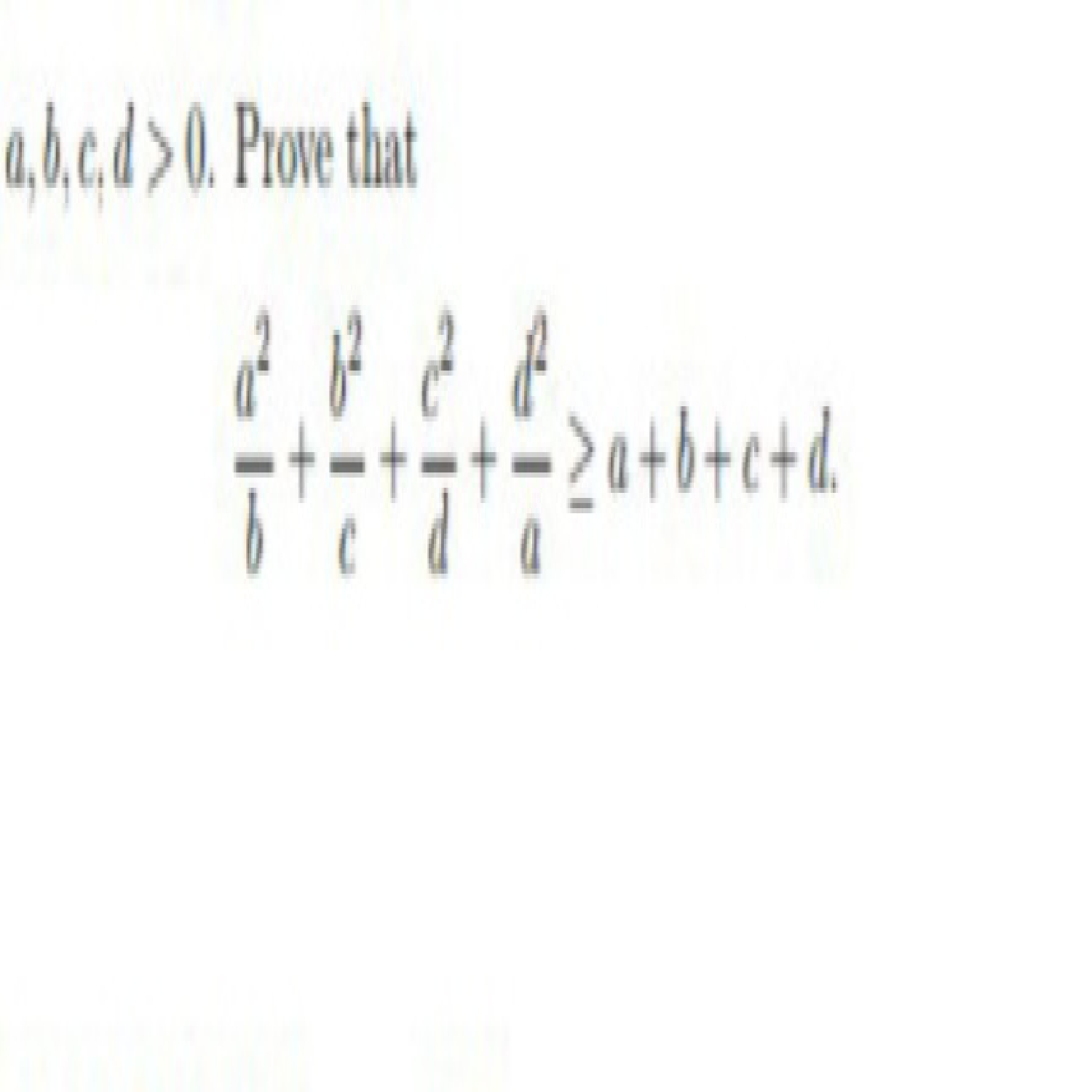
No. of integral roots of the eqn. x8 - 24 x7 - 18x5 + 39 x2 + 1155 = 0 .
two times sign change so 2 positive roots
let a,b,c be three distinct real numbers such that each of expression ax2+bx+c,bx2+cx+a,cx2+ax+b are positive for all x ε R and let
α=bc+ca+ab/a2+b2+c2 then
(A) α<4 (B) α<1 (C) α>1/4 (D) α>1
THIS IS MULTIPLE CHOICE QUESTION
if ax2+bx+c is positive for real x
then b2< 4ac similarly others
on adding all inequalities we get b2 + c2 + a2< 4(ac+ab+bc)
now get answer
4[3t+17]=10
let [ ] is greatest integer function
so 4[3t+17] = 10
or [3t+17] = 2.5
since greatest integer function can not be non integral so no t is possible.
now if [ ] is a normal bracket
then 3t+17 = 2.5 or 3t = -14.5 or t =-14.5/3 = -145/30 = -29/6
(α,β);(β,γ) &(γ,α) are respectively the roots of x²-2px+2=0, x²-2qx+3=0,x²-2rx+6=0. if α,β,γ are all positive , then the value of p+q+r is
According to the given conditions
α+β=2p (1) α*β=2 (2)
β+γ=2q (3) β*γ=3 (4)
γ+α=2r (5) γ*α=6 (6)
so α+β+γ = p+q+r (7)
and α*β*γ=6 (8)
dividing eq. (8) by (2), (4) , (6) one by one we will get α, β, γ hence we will get p+q+r
If the eqaution x^3-3x+k, always has exactly one +ve real root , then find teh minimum value of [|k|].
let f(x) = x^3-3x+k
so f'(x) = 3 x^2 - 3
on comparing with 0, x = +1, -1
on double differentiating we get that function f(x) is minimum at +1 and maximum at -1
so for getting the only +ve real root plot a graph such that it could intersect positive x axis at any point and nowhere else. From the graph it is clear that k will be negative.
at x = +1, f(x) = k-2
at x = -1, f(x) = k+2
so on the basis of given conditions k-2<0 or k<2 and k+2<0 or k<-2
finally k<-2 so [|k|] has minimum value 2
x^7 - 3x^4+2x^3-k=0, k>0 has atleast m imaginary roots then m is ?
x^7 - 3x^4+2x^3-k=0
according to sign change rule there are 3 pair of sign + -, - +, + - , see the sign before coefficient of different powers
so 3 positive real roots are confirmed
now take x = -x
we get -x^7 - 3x^4 - 2x^3 - k = 0, there is no sign change so no negative root
total real roots = 3
so imaginary roots = 4