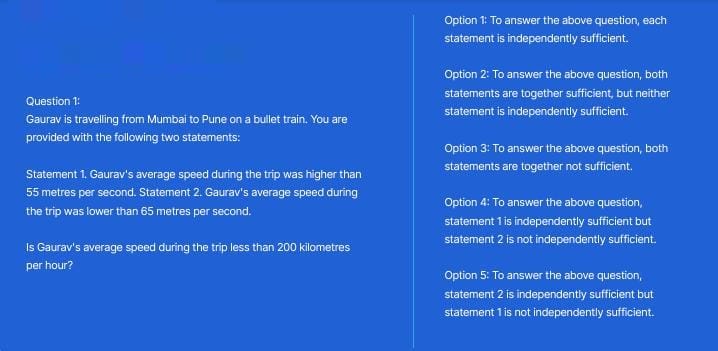
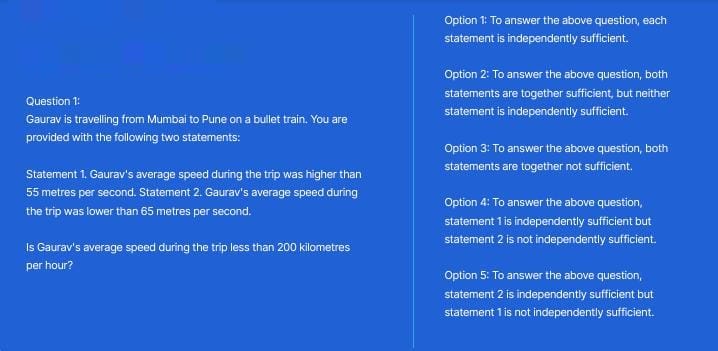
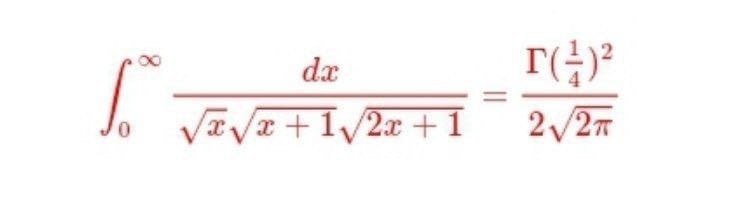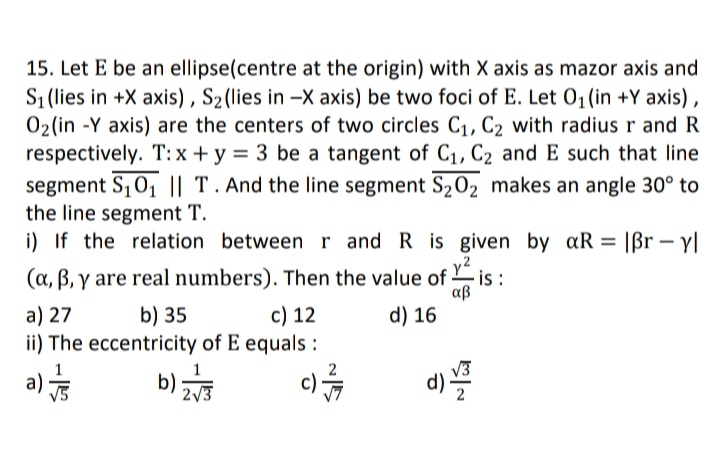166 - Questions Answers
Prove that the system of confocal conics x²/(a² + π) + y²/(b² + π) = 1, π being the parameter is self orthogonal.
Asked By: SEVAK KUMAR
is this question helpfull: 0 2
submit your answer
(iii) tan69∘+tan66∘+1=tan69∘⋅tan66∘.
Asked By: KHUSHI
is this question helpfull: 2 0
submit your answer