63 - Calculus Questions Answers
Find
lim n→∞ ⁿ√(n!) / n
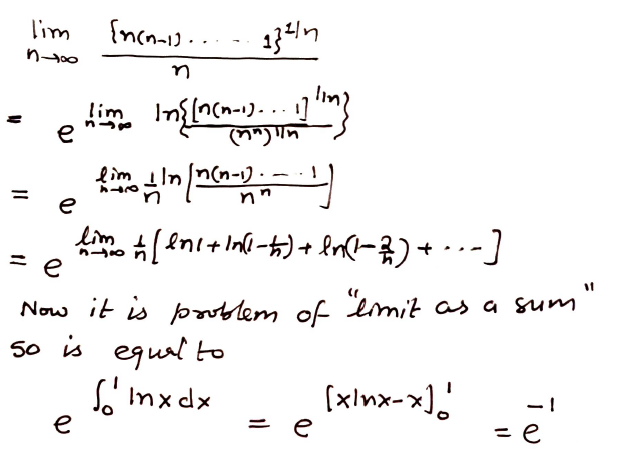
1 . Iₙ = ∫ ( 1/ ( x² + a²)ⁿ )dx
How to do this by substituting x = a tan Α
2. Is this true
∫ f(x) d(kg(x)) = k ∫ f(x) d(g(x))
where k is a constant

d/dx((1+x^2+x^4)/(1+x+x^2))=ax+b
then a=?, b=?
1+x2+x4 = (1+x+x2)(1-x+x2)
now solve
Find a formula for a function g(x) satisfying the following conditions
a) domain of g is (-∞ , ∞ ) b) range of g is [-2 , 8] c) g has a period π d) g(2) = 3
g(x) = 3-5sin(2x-4)
Let f(x) = x135 + x125 - x115 + x5 +1. If f(x) is divided by x3-x then the remainder is some function of x say g(x). Find the value of g(10)
for getting reminder put x3= x so
x135 + x125 - x115 + x5 +1 will give
x45 + x41*x2 - x38*x +x*x2 +1
x15 + x13*x2*x2 - x12*x2*x +x*x2 +1
x17 + x3 +1
x5*x2 + x + 1
x7 + x + 1
x2*x + x +1
x3 + x +1
x+x+1
2x+1
now put x = 10
How to inegrate ( In t) dt /(t-1)
let lnt = x so dt/t = dx so dt = tdx = exdx
now ∫(ln t)dt/(t-1) = ∫xexdx/(ex-1) = ∫x(ex-1+1)dx/(ex-1)
now solve
∫√tanx
let √tanx = t
so sec2xdx/2√tanx = dt
so (1+t4)dx/2t = dt
so dx = 2tdt/(1+t4)
now solve
if ƒ:R−{0} -> R, 2ƒ(x) − 3ƒ(1⁄x) = x² then ƒ(3)= ?
2ƒ(x) − 3ƒ(1⁄x) = x² (1)
so 2ƒ(1/x) − 3ƒ(x) = 1/x² (2)
multiply (1) to 2 and (2) to 3, then add the two equations, you will get f(x) then calculate f(3)
Sir/Madam,
Suddenly a question struck on my mind: 0×∞= 1 or 0?? as 1⁄0=∞.
it will be 0, assume it by considering that ∞ is a big number
for ex. 0*(1111111111111111111111111) = 0
FIND DOMAIN OF f(x)=log4log3 log2x WHERE 4,3,2 ARE BASES ?
f(x)= log4log3log2x
so 0 < log3log2x < ∞
so 1 < log2x < ∞
so 2 < x < ∞
