45 - Algebra Questions Answers
what is the range of log 203?
There should be any variabe in the question
1) Find the invariants of the matrix
0 1 0
0 0 0
0 0 0 of a linear transformation T in A(v) ?
2) Find the companion matrix of the polynomial ( x+1)2 ?
3) show that two real symmetric matrices are congruent if and only if they have the same rank and signature?
rank(A) = 1
det(A) = 0
trace(A) = 0
The matrix is not symmetric.
characteristic polynomial of the given matrix is x3
companion matrix of the polynomial (x+1)2
0 1
-1 -2
A real symmetric matrix of rank r is congruent over the field of real numbers to a canonical matrix
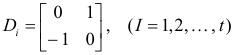
The integer p is called the index of the matrix and s = p - (r - p) is called the signature.
The index of a symmetric or Hermitian matrix is the number of positive elements when it is transformed to a diagonal matrix. The signature is the number of positive terms diminished by the number of negative terms and the total number of nonzero terms is the rank.
now solve it
The sum of three positive real numbers x, y and z is 9. If the largest positive difference between any 2 of the 3 numbers is 5 and these 3 numbers are in arithmetic progression then the product of these 3 numbers will be what .please tell me.
let the numbers are a-d, a, a+d
then according to the given condition a-d+a+a+d = 9 so 3a = 9 so a = 3
and [a+d]-[a-d] = 5 so 2d = 5 so d =5/2
now solve
number of real values of x satisfying 2log2(x+7x+1)+log2(x+1x-1)=1 is
given eq. can be written as log2 [(x+7)/(x+1)]2 + log2 [(x+1)/(x-1)] = 1
or log2 [(x+7)2(x+1)/(x+1)2(x-1)] = 1
or log2 [(x+7)2/(x2-1)] = 1
or (x+7)2/(x2-1) = 2
or x2 + 14x +49 = 2x2 - 2
or x2-14x -51 = 0
or x = -3, 17
since at x = -3 first part will become negative inside root so it will not be a root.
so only 1 root
If the letters of the word are arranged as in dictionary, find the rank of the word INDIA.
On arranging the letters in ascending order we will get
A D I I N
total no of words = 5*4*3*2*1/2*1 = 60
rank = (60/5)*2 + (24/4)*3 + (6/3)*1 + (2/2)*1 + 1 = 24+18+2+1+1 = 46
here 60/5 means total words/ total letters and 2 is here because in INDIA, I is first letters and this comes at 3rd and 4th place in ascending order arrangement so total letters before it are 2. similarly 24 stands for total words after removing I from the spelling of INDIA and etc
4[3t+17]=10
let [ ] is greatest integer function
so 4[3t+17] = 10
or [3t+17] = 2.5
since greatest integer function can not be non integral so no t is possible.
now if [ ] is a normal bracket
then 3t+17 = 2.5 or 3t = -14.5 or t =-14.5/3 = -145/30 = -29/6
The number of solutions of : 4x²-4x+2 = sin² y & x²+y² ≤ 3 are ? (please solve it graphically i am getting one solution by using graph but the answer is 2)
Given eq. can be written as (2x-1)2 + 1 = sin2y
and max. of siny is 1 so only possible value of x = 1/2
and possible values of y = ±nπ/2 where n is odd integer
but by drawing the circle of 2nd eq. we find that only y = ±π/2 are possible values so answer will be 2
What is the range of the function y = (e^-x)/ (1+[x]) is ?
Domain of the given function is (-∞, -1) υ [0, ∞)
Now at x=0, y=1
and at x=∞, y=0
similarly left limiting value of y = -e
and for x=-∞, y=-∞
so range is (-∞, -e] υ (0, 1]
The AM of two positive numbers a & b exceeds their GM by 3/2 & the GM exceeds the HM by 6/5 such that a+b= α , |a-b|=β , then which of them are correct,
1) α + β² = 96 2) α + β² =74 3)α²+β = 234 4)α²+β = 84
(a+b)/2 = √ab + 3/2 (1) or a+b = 2√ab + 3
√ab = 2ab/(a+b) + 6/5 (2) or 5(a+b)√ab = 10ab + 6(a+b)
on solving these 2 we get 5[2√ab + 3]√ab = 10ab + 6[2√ab + 3]
or 10ab + 15√ab = 10ab + 12√ab + 18
or 3√ab = 18 or ab = 36 and a+b = 15 = α
so a-b = √(225 - 144) = √81 = 9 = β
(α,β);(β,γ) &(γ,α) are respectively the roots of x²-2px+2=0, x²-2qx+3=0,x²-2rx+6=0. if α,β,γ are all positive , then the value of p+q+r is
According to the given conditions
α+β=2p (1) α*β=2 (2)
β+γ=2q (3) β*γ=3 (4)
γ+α=2r (5) γ*α=6 (6)
so α+β+γ = p+q+r (7)
and α*β*γ=6 (8)
dividing eq. (8) by (2), (4) , (6) one by one we will get α, β, γ hence we will get p+q+r