166 - Questions Answers

Maths >> Calculus >> Applications of integrations Others

y=px+a/p

Asked By: FRANCISBHORGIA

is this question helpfull: 2 0 submit your answer

Joshi sir comment

this is a special type of differential equation in which p = dy/dx

its solution will be y = cx+(a/c) here c is a constant

Maths >> Calculus >> Applications of integrations IIT JEE

y-xp=x+yp

Asked By: FRANCISBHORGIA

is this question helpfull: 1 1 submit your answer

Joshi sir comment

on applying p = dy/dx

(ydx-xdy)/dx = (xdx+ydy)/dx

or ydx-xdy = xdx+ydy

or dy/dx = (y-x)/(y+x)

now it is homogeneous

Maths >> Algebra >> Matrices and Determinant Others

1) Find the invariants of the matrix

0 1 0

0 0 0

0 0 0 of a linear transformation T in A(v) ?

2) Find the companion matrix of the polynomial ( x+1)² ?

3) show that two real symmetric matrices are congruent if and only if they have the same rank and signature?

Asked By: INDU.R.PAI

is this question helpfull: 5 1 submit your answer

Joshi sir comment

rank(A) = 1
det(A) = 0
trace(A) = 0
The matrix is not symmetric.

characteristic polynomial of the given matrix is x³

companion matrix of the polynomial (x+1)²

0 1

-1 -2

A real symmetric matrix of rank r is congruent over the field of real numbers to a canonical matrix

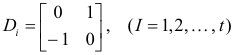
The integer p is called the index of the matrix and s = p - (r - p) is called the signature.

The index of a symmetric or Hermitian matrix is the number of positive elements when it is transformed to a diagonal matrix. The signature is the number of positive terms diminished by the number of negative terms and the total number of nonzero terms is the rank.

now solve it

Maths >> Trigonometry >> Trigonometrical Equations IIT JEE

A regular hexagon and a regular dodecagon are inscribed in the same circle. if the side of the dodecagon is (√3-1), then the side of hexagon is

Asked By: HEMA RANI

is this question helpfull: 2 0 submit your answer

Joshi sir comment

for dodecagon sin(2π/40) = (a/2)/r so r = (a/2)/ sin(π/20)

now for hexagon sin(2π/12) = (x/2)/r so x/2 = r sin(π/6) = (a/2) sin(π/6)/ sin(π/20)

so x = (√3-1) (1/2) / ((√5-1)/4) here sin(π/20) = (√5-1)/4

or x = 4(√3-1) / 2(√5-1)

now solve it for further simplification

Maths >> Trigonometry >> General Trigonometry Board Exam

What are trigonometrical identities?

Asked By: SIDDHANT KAPOOR

is this question helpfull: 3 2 submit your answer

Joshi sir comment

sin²A + cos²A = 1 and two similar formulae in terms of tanA, cotA, secA and cosecA

these are identities because these are true for all values of A

Maths >> Trigonometry >> General Trigonometry IIT JEE

if secA-tanA=3

then find the value of (5cosA+4cotB)??

jus a hint

Asked By: AMBUJ SINGLA Solved By: NIKHIL VARSHNEY

is this question helpfull: 2 1 read solutions ( 1 ) | submit your answer

Joshi sir comment

First replace cotB by cotA.

because it is wrongly printed by you.

answer by NIKHIL is correct

Maths >> Algebra >> Sequence and Series Others

The sum of three positive real numbers x, y and z is 9. If the largest positive difference between any 2 of the 3 numbers is 5 and these 3 numbers are in arithmetic progression then the product of these 3 numbers will be what .please tell me.

Asked By: S.NANDHINI

is this question helpfull: 10 2 read solutions ( 1 ) | submit your answer

Joshi sir comment

let the numbers are a-d, a, a+d

then according to the given condition a-d+a+a+d = 9 so 3a = 9 so a = 3

and [a+d]-[a-d] = 5 so 2d = 5 so d =5/2

now solve

Maths >> Calculus >> Limit Continuity and Differentiability Others

Importance High!!!!!!!!!!!!!!!!!

Dear Sir / Madam

Myself Rajeev Shrivastava, I am putting a signs series in front of you which based on numbers from 01 to 100. Actually I want to know that what reason of behind Approx equability of signs is

(++), (+-), (--) & (-+) at end of the month or year between the below mentioned.

Let's define a kind of mapping:
0↔1
2↔3
4↔5
6↔7
8↔9

(+) means: an Even number
(-) means: an Odd number

I simply say: for any EO (+-) it exists an OE (-+) which is paired to.
And that's true since each E is mapped to a O and vice versa (1 to 1 relation where "f(f(x))=x" ) !
E.g.: 29 ↔ 83

There is 25 numbers in the EO (+-) group, so 25 in OE (+-).
There is 25 numbers in the EE (++) group, so 25 in OO (--).

Picking a number at random between 01 and 100 inclusive is choosing equitably in EO, OE, EE or OO group. (25% for each)

So, I really need of your help to solve a puzzle please. I just am trying to make you understand what type of solution I need:

There are some results for your review:

MONTH	DATE	DAY	FIRST_SERIES		SECOND_SERIES		FIRST_SERIES	SECOND_SERIES
APR	1	SUN	+	-	-	+	+-	-+
APR	2	MON	+	+	-	+	++	-+
APR	3	TUE	+	-	+	-	+-	+-
APR	4	WED	+	+	+	+	++	++
APR	5	THU	-	+	-	+	-+	-+
APR	6	FRI	+	+	+	-	++	+-
APR	7	SAT	+	-	-	+	+-	-+
APR	8	SUN	-	+	+	-	-+	+-
APR	9	MON	-	+	-	+	-+	-+
APR	10	TUE	+	+	+	+	++	++
APR	11	WED	+	+	-	-	++	--
APR	12	THU	-	+	-	-	-+	--
APR	13	FRI	+	+	+	+	++	++
APR	14	SAT	+	-	+	-	+-	+-
APR	15	SUN	+	-	+	-	+-	+-
APR	16	MON	-	-	+	+	--	++
APR	17	TUE	-	-	+	+	--	++
APR	18	WED
APR	19	THU
APR	20	FRI
APR	21	SAT
APR	22
APR	23

(Complete sheets for the year 2011 and 2012 are attached with this mail)

You can see that there are two times falls in a day of pair make by even (+) and odd (-) signs, i.e. (++), (+-), (--) & (-+) as above said.

The total of pair combination signs become approx equal to each other at the end of the month or year (every year- so, I am sending you attachment to go through the year’s result).

By this analysis:

1- I want to know that what is the relation between current falling signs and past fell signs.

2- How can I come to know, what type of combination of sign would be any particular date or day.

3- As you can seen on 22^nd and 23^rd April’2012 I don’t know what combination of sign is.

4- There is surety that there is some relation between current First fall of combination of signs and past fall or First fall of combination of signs and Second fall of combination of signs.

Please help me to how come to know what type of fall may be for next day by reviewing past or first combination of signs. So reply or elaborate me with an example.

I would be very grateful to you till entire life.

Regards

RAJEEV SHRIVASTAVA

Importance High!!!!!!!!!!!!!!!!!

Dear Sir / Madam

Myself Rajeev Shrivastava, I am putting a signs series in front of you which based on numbers from 01 to 100. Actually I want to know that what reason of behind Approx equability of signs is

(++), (+-), (--) & (-+) at end of the month or year between the below mentioned.

Let's define a kind of mapping:
0↔1
2↔3
4↔5
6↔7
8↔9

(+) means: an Even number
(-) means: an Odd number

I simply say: for any EO (+-) it exists an OE (-+) which is paired to.
And that's true since each E is mapped to a O and vice versa (1 to 1 relation where "f(f(x))=x" ) !
E.g.: 29 ↔ 83

There is 25 numbers in the EO (+-) group, so 25 in OE (+-).
There is 25 numbers in the EE (++) group, so 25 in OO (--).

Picking a number at random between 01 and 100 inclusive is choosing equitably in EO, OE, EE or OO group. (25% for each)

So, I really need of your help to solve a puzzle please. I just am trying to make you understand what type of solution I need:

There are some results for your review:

MONTH	DATE	DAY	FIRST_SERIES		SECOND_SERIES		FIRST_SERIES	SECOND_SERIES
APR	1	SUN	+	-	-	+	+-	-+
APR	2	MON	+	+	-	+	++	-+
APR	3	TUE	+	-	+	-	+-	+-
APR	4	WED	+	+	+	+	++	++
APR	5	THU	-	+	-	+	-+	-+
APR	6	FRI	+	+	+	-	++	+-
APR	7	SAT	+	-	-	+	+-	-+
APR	8	SUN	-	+	+	-	-+	+-
APR	9	MON	-	+	-	+	-+	-+
APR	10	TUE	+	+	+	+	++	++
APR	11	WED	+	+	-	-	++	--
APR	12	THU	-	+	-	-	-+	--
APR	13	FRI	+	+	+	+	++	++
APR	14	SAT	+	-	+	-	+-	+-
APR	15	SUN	+	-	+	-	+-	+-
APR	16	MON	-	-	+	+	--	++
APR	17	TUE	-	-	+	+	--	++
APR	18	WED
APR	19	THU
APR	20	FRI
APR	21	SAT
APR	22
APR	23

(Complete sheets for the year 2011 and 2012 are attached with this mail)

You can see that there are two times falls in a day of pair make by even (+) and odd (-) signs, i.e. (++), (+-), (--) & (-+) as above said.

The total of pair combination signs become approx equal to each other at the end of the month or year (every year- so, I am sending you attachment to go through the year’s result).

By this analysis:

1- I want to know that what is the relation between current falling signs and past fell signs.

2- How can I come to know, what type of combination of sign would be any particular date or day.

3- As you can seen on 22^nd and 23^rd April’2012 I don’t know what combination of sign is.

4- There is surety that there is some relation between current First fall of combination of signs and past fall or First fall of combination of signs and Second fall of combination of signs.

Please help me to how come to know what type of fall may be for next day by reviewing past or first combination of signs. So reply or elaborate me with an example.

I would be very grateful to you till entire life.

Regards

RAJEEV SHRIVASTAVA

Asked By: RAJEEV SHRIVASTAVA

is this question helpfull: 8 1 read solutions ( 1 ) | submit your answer

Joshi sir comment

If you are making the sequence on the basis of dates then you should take signs accordingly then you can make this sequence for many years

for example if you take 23 june then first sign series will be +-, + for even number and - for odd number , now as conversion rule as you gave in your explanation 23 will be converted to 32 so second series will be -+

similarly you can make it for any date

for example 29 december first series will be +- and its conversion is 38 so next series will be -+

if you are thinking something else then explain your question correctly

Maths >> Calculus >> Differential Equations IIT JEE

how to find differential eqn. of all conics whose axes coincide with coordinate axes?? tell me the eqn. of tht. conic

Asked By: SHALINI SINGH

is this question helpfull: 10 4 submit your answer

Joshi sir comment

Parabola eq. y² = 4ax ,

on differentiating this eq. with respect to x we get 2y(dy/dx) = 4a

on taking this value of 4a in eq. y²= 4ax we will get the differential eq. of parabola.

similarly for ellipse x²/a² + y²/b² = 1

on differentiaing this eq. twice we will get two additional eq.

by solving these eq. get an eq. free from a and b, this will be the differential eq. of the ellipse.

similarly for hyperbola

Maths >> Trigonometry >> General Trigonometry IIT JEE

Which of the following angles are co-terminal angles: 480 , -240 or 600

how can we get it which is co-terminal and what does co-terminal means?????

Asked By: AMBUJ SINGLA

is this question helpfull: 1 1 submit your answer

Joshi sir comment

Coterminal angles are angles in standard position (angles with the initial side on the positive x-axis) that have a common terminal side. For example 30°, –330° and 390° are all coterminal.

To find a positive and a negative angle coterminal with a given angle, you can add and subtract 360° if the angle is measured in degrees or 2π if the angle is measured in radians.

480 and -240 are co terminal angles because 480-360 = 120 and -240+360 = 120

166 - Questions Answers

Login Here

Forget Password

Registration Form