Chord of contact: the chord joining the points of contact of the two tangents to a conic drawn from a given point, outside it, is called the chord of contact of tangents.
Pole and Polar:
Polar of a point with respect to a circle: through a point P(x1,y1) (inside or outside a circle) there be drawn any straight line to meet the given circle a Q and R, the locus of the point of intersection of the tangents at Q and R is called the polar of point P and P is the called the pole of the polar.
Diameter – definition as a locus: the locus of the middle points of a system of parallel chords of a circle is called a diameter of the circle.
Common chord of two circles: The chord joining the points of intersection of two given circles is called their common chord.
Angle of intersection of two curves: If the two curves C1 and C2 intersect at a point P and PT1 and PT2 be the tangents to the two curves C1 and C2 respectively at P. Then the angle between the tangents at P is called the angle of intersection of the two curves at the point of intersection.
Orthogonal curves: Two curves are said to intersect orthogonally when the two tangents at the common point are at right angles.
Radical axis: the radical axis of two circles is the locus of a point which moves in such a way that the lengths of the tangents drawn from it to the two circles are equal.
Radical centre: The point of concurrence of the radical axes of three circles whose centres are non-collinear, taken in pairs, is called the radical centre of the circles.
Coaxial system of circles: A system of circles, every pair of which has the same radical axis is called a coaxial system of circles.
160 - Mathematics Questions Answers
Tips about circle
Asked By: ADMINISTRATOR
is this question helpfull: 5 0
submit your answer
Solution by Joshi sir
Circle - Important Definitions
Director circle: the locus of the point of intersection of two perpendicular tangents to a given conic is known as its director circle.
(i) Circle passes through origin
So radius = a² = h²+k²
(x-h)²+(y-k)² = h²+k²
(ii)Circle touches the x axis
C(h,k) centre, a = radius
To satisfy a = k
So equation is
(x-h)²+(y-a)² = a²
(iii)Circle touches the y axis
C(h,k) centre, a = radius
To satisfy a = h
So equation is
(x-a)²+(y-k)² = a²
(iv) When the circle touches both axes
then h = k = a
(x-a)²+(y-a)² = a²
(v) When the circle passes through the origin and centre is on x-axis.
C(h,k) centre, a = radius
As centre is on x axis y coordinate is zero. So k = 0.
As circle is passing through origin a = h
(x-a)²+ y² = a²
(vi) When the circle passes through the origin and centre is on y-axis.
C(h,k) centre, a = radius
As centre is on y axis x coordinate is zero. So h = 0.
As circle is passing through origin a = k
x²+(y-a)² = a²
(x-h)²+(y-k)² = h²+k²
(ii)Circle touches the x axis
C(h,k) centre, a = radius
To satisfy a = k
So equation is
(x-h)²+(y-a)² = a²
(iii)Circle touches the y axis
C(h,k) centre, a = radius
To satisfy a = h
So equation is
(x-a)²+(y-k)² = a²
(iv) When the circle touches both axes
then h = k = a
(x-a)²+(y-a)² = a²
(v) When the circle passes through the origin and centre is on x-axis.
C(h,k) centre, a = radius
As centre is on x axis y coordinate is zero. So k = 0.
As circle is passing through origin a = h
(x-a)²+ y² = a²
(vi) When the circle passes through the origin and centre is on y-axis.
C(h,k) centre, a = radius
As centre is on y axis x coordinate is zero. So h = 0.
As circle is passing through origin a = k
x²+(y-a)² = a²
x²+y²+2gx+2fy+c = 0
Centre of this circle = (-g,-f)
Radius = √(g²+f²-c)
Centre of this circle = (-g,-f)
Radius = √(g²+f²-c)
If (x1,y1) and (x2,y2) are coordinates of end points of the diameter
then the equation of the circle is
(x - x1)(x - x2)+(y - y1)(y- y2) = 0
then the equation of the circle is
(x - x1)(x - x2)+(y - y1)(y- y2) = 0
Intercept of a circle is a line that is a chord which is part of x axis
Intercepts for the circle x²+y²+2gx+2fy+c = 0
length of intercept on x- axis = 2√(g²-c)(You get it by putting y = 0)
length of intercept on y- axis = 2√(f²-c)(You get it by putting x = 0)
Intercepts for the circle x²+y²+2gx+2fy+c = 0
length of intercept on x- axis = 2√(g²-c)(You get it by putting y = 0)
length of intercept on y- axis = 2√(f²-c)(You get it by putting x = 0)
Is a point in the circle, on the circle or outside the circle
If the point is P find distance between the centre of the circle C and point P.
If the radius of the circle be R
CP is greater than R implies point is outside the circle.
CP = R implies point is on the circle
CP is less than R implies point is inside.
If the point is P find distance between the centre of the circle C and point P.
If the radius of the circle be R
CP is greater than R implies point is outside the circle.
CP = R implies point is on the circle
CP is less than R implies point is inside.
Parametric equations of x² + y² = r²
x = r cos θ, y = r sin θ
Parametric equations of (x-a)² + (y-b)² = r²
x = a + r cos θ, y = b + r sin θ
x = r cos θ, y = r sin θ
Parametric equations of (x-a)² + (y-b)² = r²
x = a + r cos θ, y = b + r sin θ
Equation of the circle: x² + y² = a²
Equation of the line: y = mx+c
A line does not intersect a circle if the length of the perpendicular to the line from the centre of the circle is greater than the radius of the circle.
|c/√(1+m²)|>a
A line intersects a circle if the length of the perpendicular to the line from the centre of the circle is less than the radius of the circle.
|c/√(1+m²)|<a
A line touches a circle if the length of the perpendicular to the line from the centre of the circle is equal to the radius of the circle.
|c/√(1+m²)| = a
Equation of the line: y = mx+c
A line does not intersect a circle if the length of the perpendicular to the line from the centre of the circle is greater than the radius of the circle.
|c/√(1+m²)|>a
A line intersects a circle if the length of the perpendicular to the line from the centre of the circle is less than the radius of the circle.
|c/√(1+m²)|<a
A line touches a circle if the length of the perpendicular to the line from the centre of the circle is equal to the radius of the circle.
|c/√(1+m²)| = a
Equation of the circle: x² + y² = a²
Equation of the line: y = mx+c
A line intersects a circle if the length of the perpendicular to the line from the centre of the circle is less than the radius of the circle.
If it intercepts, the length of the intercept is
2√([[a²(1+m²)-c²]/(1+m²) ]
Equation of the line: y = mx+c
A line intersects a circle if the length of the perpendicular to the line from the centre of the circle is less than the radius of the circle.
If it intercepts, the length of the intercept is
2√([[a²(1+m²)-c²]/(1+m²) ]
Tangent to a circle at a given point
Condition of tangency:
The line y = mx+c is tangent to a circle x² + y² = a² if the length of the intercept is zero.
That means 2√([[a²(1+m²)-c²]/(1+m²) ] = 0
=> a²(1+m²)-c² = 0
=> c = ±a√(1+m²)
Slope form:
The equation of a tangent of slope m to the circle x² + y² = a² is
Y = mx±a√(1+m²) (Value of c from tangent condition).
The coordinate of the point of contact are (±am/√(1+m²), ±a/√(1+m²)
The line y = mx+c is tangent to a circle x² + y² = a² if the length of the intercept is zero.
That means 2√([[a²(1+m²)-c²]/(1+m²) ] = 0
=> a²(1+m²)-c² = 0
=> c = ±a√(1+m²)
Slope form:
The equation of a tangent of slope m to the circle x² + y² = a² is
Y = mx±a√(1+m²) (Value of c from tangent condition).
The coordinate of the point of contact are (±am/√(1+m²), ±a/√(1+m²)
Point form:
The equation of a tangent at the point (x1,y1) to the circle x² + y²+2gx+2fy+c = 0 is
xx1 + yy1 +g(x+x1)+f(y+y1) +c = 0
If slope of the tangent is m, then the slope of the normal is –(1/m)
The length of a tangent from the point (x1,y1) to the circle x² + y²+2gx+2fy+c = 0 is equal to √( x1² + y1²+2gx1+2fy1+c)
Let the point be (x1,y1) and the circle be x² + y² = a²
Two tangents can be drawn.
The tangent will be of the form y = mx+a√(1+m²)
And the two values of m for the pair is to be found by solving the quadratic equation
m²(x1²-a²) -2mx1y1 +(y1²-a²) = 0
Two tangents can be drawn.
The tangent will be of the form y = mx+a√(1+m²)
And the two values of m for the pair is to be found by solving the quadratic equation
m²(x1²-a²) -2mx1y1 +(y1²-a²) = 0
The equation for pair of tangents from the point (x1,y1) to the circle x² + y²+2gx+2fy+c = 0 is given by
(x² + y²+2gx+2fy+c) (x1² + y1²+2gx1+2fy1+c) = (xx1 + yy1 +g(x+x1)+f(y+y1) +c) ²
Expressed as SS’ = T²
(x² + y²+2gx+2fy+c) (x1² + y1²+2gx1+2fy1+c) = (xx1 + yy1 +g(x+x1)+f(y+y1) +c) ²
Expressed as SS’ = T²
Director circle: the locus of the point of intersection of two perpendicular tangents to a given conic is known as its director circle.
Equation of director circle of the circle x² + y² = a² is x² + y² = 2a²
Equation of director circle of the circle x² + y² = a² is x² + y² = 2a²
The equation of the chord of contact of tangents drawn from a point (x1,y1) outside the circle to the circle x² + y² = a² is xx1+yy1 = a².
Polar of a point with respect to a circle: If through a point P(x1,y1) (inside or outside a circle) there be drawn any straight line to meet the given circle a Q and R, the locus of the point of intersection (T) of the tangents at Q and R is called the polar of point P and P is the called the pole of the polar.
Polar is the locus of point and pole is a point with respect to which polar is determined.
Equation to the polar of the point (x1,y1) w.r.t. to the circle x² + y² = a² is
xx1+yy1= a²
The polar of the point (x1,y1) w.r.t. to the circle x² + y²+2gx+2fy+c = 0 is given by
(xx1+ yy1 +g(x+x1)+f(y+y1) +c) = 0
The equation is same as the equation for the tangent to the circle at a point (x1,y1) on the circle.
Polar is the locus of point and pole is a point with respect to which polar is determined.
Equation to the polar of the point (x1,y1) w.r.t. to the circle x² + y² = a² is
xx1+yy1= a²
The polar of the point (x1,y1) w.r.t. to the circle x² + y²+2gx+2fy+c = 0 is given by
(xx1+ yy1 +g(x+x1)+f(y+y1) +c) = 0
The equation is same as the equation for the tangent to the circle at a point (x1,y1) on the circle.
The equation of the chord of the circle x² + y²+2gx+2fy+c = 0 bisected at the point (x1,y1) is given by
T = S’
(xx1 + yy1+g(x+x1)+f(y+y1) +c) = x1² + y1²+2gx1+2fy1+c
T = S’
(xx1 + yy1+g(x+x1)+f(y+y1) +c) = x1² + y1²+2gx1+2fy1+c
Equation of the diameter bisecting parallel chords y =mx+c ( c is a parameter i.e., varies to give various chords) of the circle x² + y² = a² is x+my = 0
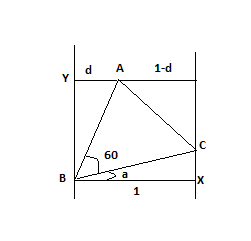
The distance between two parallel lines is 1.A point 'A' is chosen to lie between the lines at a distance 'd' from the first line. Triangle ABC is an eqilateral triangle with 'B" on one line and 'C' on the other line.Then AB is equal to(in terms of d).
Asked By: AMIT DAS
is this question helpfull: 9 0
submit your answer
Joshi sir comment
In triangle BCX
BC = seca
so AB = seca
now in triangle ABY
cos(60+a) = d/seca
so 1/2 cosa - √3/2 sina = d cosa
or tana = (1-2d)/√3
now calculate seca
Let a number n have its base -7 representation as n= 1223334444. the highest power of 7, that divides the number n! is
Asked By: AMIT DAS
Joshi sir comment
n = (1223334444)7 = 1*79 + 2*78 + 2*77 + 3*76 + 3*75 + 3*74 + 4*73 + 4*72 + 4*71 + 4*70
so if we will divide n! by 7x we will get 1*78 + 2*77 + 2*76 + 3*75 + 3*74 + 3*73 + 4*72 + 4*71 + 4*70 as x
A light example
if we divide (1*72 + 2*71 + 3*70)! by 7x we get x = 1*71 + 2*70 = 9
- what is the integration of cosx 2
Asked By: VIKRANT KUMAR
is this question helpfull: 4 0
submit your answer
Joshi sir comment
cosx2 = (cos2)x
so ∫ (cos2)x dx = (cos2) x / logecos2
Solution by Joshi sir
cosx2 = (cos2)x
so ∫ (cos2)x dx = (cos2) x / logecos2 + C formula ∫axdx = ax/logea
let z be a complex number satisfying |z-3|=|z-4i|, then find the least possible value of 10|z|.
Asked By: AMIT DAS
Joshi sir comment
In |z-3|=|z-4i|, z represents all points lying on the perpendicular bisector of the line joining 3 and 4i in x-y plane. In this perpendicular bisector, if we draw a perpendicular then it will be the minimum magnitude of z. Construct this as a diagram we will get
sinθ = |z| / (7/8)
or |z| = (7/8)(4/5) = 7/10
If the eqaution x^3-3x+k, always has exactly one +ve real root , then find teh minimum value of [|k|].
Asked By: AMIT DAS
is this question helpfull: 2 1
submit your answer
Joshi sir comment
let f(x) = x^3-3x+k
so f'(x) = 3 x^2 - 3
on comparing with 0, x = +1, -1
on double differentiating we get that function f(x) is minimum at +1 and maximum at -1
so for getting the only +ve real root plot a graph such that it could intersect positive x axis at any point and nowhere else. From the graph it is clear that k will be negative.
at x = +1, f(x) = k-2
at x = -1, f(x) = k+2
so on the basis of given conditions k-2<0 or k<2 and k+2<0 or k<-2
finally k<-2 so [|k|] has minimum value 2
x^7 - 3x^4+2x^3-k=0, k>0 has atleast m imaginary roots then m is ?
Asked By: AMIT DAS
is this question helpfull: 2 0
submit your answer
Joshi sir comment
x^7 - 3x^4+2x^3-k=0
according to sign change rule there are 3 pair of sign + -, - +, + - , see the sign before coefficient of different powers
so 3 positive real roots are confirmed
now take x = -x
we get -x^7 - 3x^4 - 2x^3 - k = 0, there is no sign change so no negative root
total real roots = 3
so imaginary roots = 4
find the value of [(1+0.0001)10000] WHERE [.] REPRESENTS GREATEST INTEGER FONCTION.
Asked By: SHUBHAM VED
is this question helpfull: 3 0
submit your answer
Joshi sir comment
(1 + 0.0001) 10000 = 1 + 10000*0.0001 + other terms = greater then 2
besides it lim x->0 (1+x)1/x = e = less then 3
it means the given expression is more then 2 but less then 3
so 2 will be the answer
A housewife buys a dozen eggs of which two turn out to be bad. She chooses four eggs for breakfast. Find thd chance that she chooses (1) all good eggs (2)three good and one bad (3)two good and two bad (4)at least one bad egg.
Asked By: SAHDEV SINGH
Joshi sir comment
1) (10/12)(9/11)(8/10)(7/9)
2) 4(10/12)(9/11)(8/10)(2/9)
3) (4*3/2)(10/12)(9/11)(2/10)(1/9)
4) 1 - (10/12)(9/11)(8/10)(7/9)
consider 5 american couples and 2 indian couples sitting beside each other in n2 tables in the form of log5x.
Asked By: AKSHAY
is this question helpfull: 12 3
submit your answer
Joshi sir comment
Please send the complete question