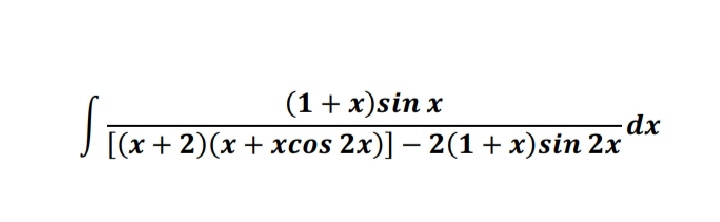166 - Mathematics Questions Answers

Asked By: TONY

is this question helpfull: 0 0 submit your answer

Joshi sir comment

Asked By: TONY

is this question helpfull: 0 0 submit your answer

Asked By: TONY

is this question helpfull: 0 0 submit your answer

Asked By: TONY

is this question helpfull: 0 0 submit your answer

Asked By: TONY

is this question helpfull: 0 0 submit your answer

Asked By: RISHABH SHUKLA

is this question helpfull: 0 0 read solutions ( 1 ) | submit your answer

Joshi sir comment

Asked By: RAM KUMAR

is this question helpfull: 0 0 submit your answer

Asked By: RAM KUMAR

is this question helpfull: 0 0 submit your answer

Solve in integers the equation $x^{2} + y^{2} + x y = {(\frac{x + y}{3} + 1)}^{3}$

Asked By: RATHER NOT SAY

is this question helpfull: 0 0 submit your answer

Joshi sir comment

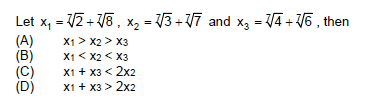
Asked By: HARDIK

is this question helpfull: 2 1 read solutions ( 1 ) | submit your answer

Joshi sir comment

Your Full Name :

Your Email Address :

Country :

State :