166 - Mathematics Questions Answers

Asked By: LUFFY
is this question helpfull: 0 0
submit your answer
Joshi sir comment
Let the lines in the pair are m1x-y=0 and m2x-y=0Find perpendiculars from (x,,y,) on lines and calculate their sumUse formulae m1+m2 = -2hb and m1m2= abInform for any issue
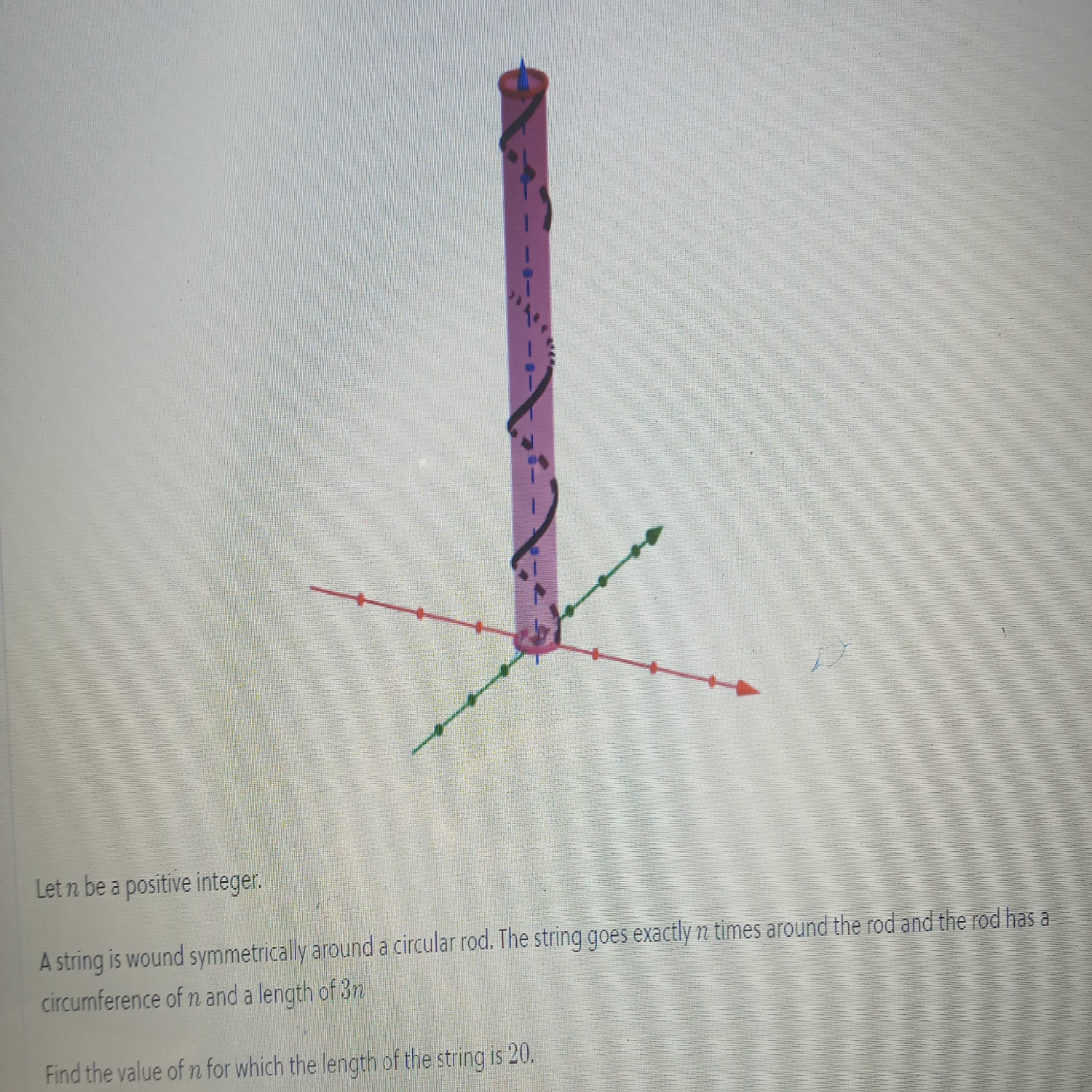
Asked By: LUFFY
Joshi sir comment
length for one turn = 3
Draw diagonal of a rectangle then turn it as a cylinder, you will get the construction given in the question.

Asked By: LUFFY
is this question helpfull: 0 0
submit your answer
Joshi sir comment

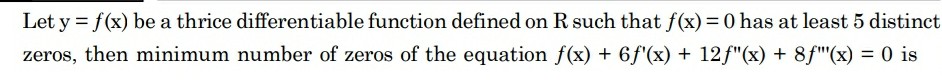
Asked By: KANDUKURI ASHISH
is this question helpfull: 2 0
submit your answer
Joshi sir comment

Asked By: ASHLOK
is this question helpfull: 2 0
submit your answer
Joshi sir comment
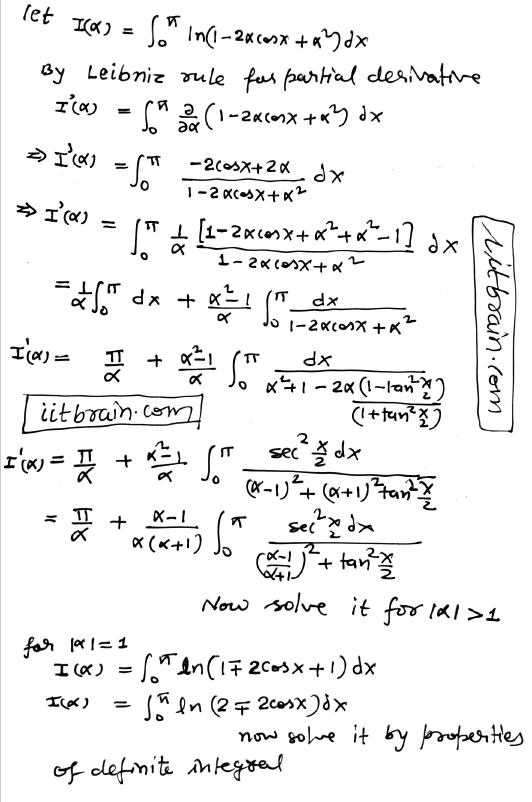
Find
lim n→∞ ⁿ√(n!) / n
Asked By: LUFFY
is this question helpfull: 1 0
submit your answer
Joshi sir comment
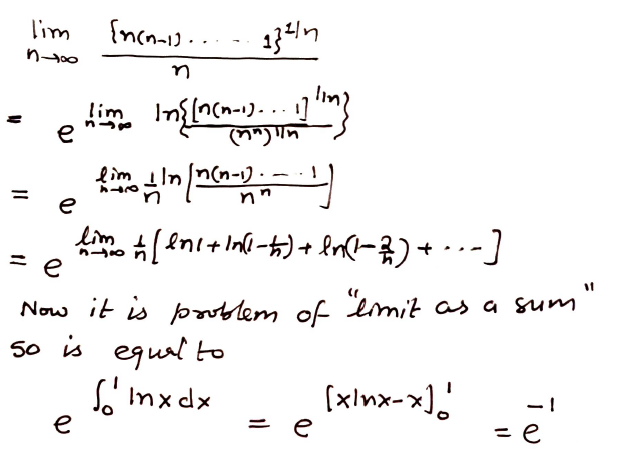

Asked By: LUFFY
is this question helpfull: 0 0
submit your answer
Joshi sir comment
Find Sum to n terms
x/1-x² + x²/1-x⁴ + x⁴/1-x⁸ + ....
Asked By: LUFFY
is this question helpfull: 3 0
submit your answer
Joshi sir comment
1 . Iₙ = ∫ ( 1/ ( x² + a²)ⁿ )dx
How to do this by substituting x = a tan Α
2. Is this true
∫ f(x) d(kg(x)) = k ∫ f(x) d(g(x))
where k is a constant
Asked By: LUFFY
is this question helpfull: 3 0
submit your answer
Solution by Joshi sir

d/dx((1+x^2+x^4)/(1+x+x^2))=ax+b
then a=?, b=?
Asked By: RAJIV
Joshi sir comment
1+x2+x4 = (1+x+x2)(1-x+x2)
now solve
