166 - Mathematics Questions Answers

Asked By: HARDIK
is this question helpfull: 0 0
submit your answer
Joshi sir comment


Asked By: LUFFY
is this question helpfull: 0 0
submit your answer
Joshi sir comment

There are 8 distinct boxes and each box can hold any number of balls. A child having 4 identical balls randomly choose four boxes. Then another child having four balls, identical to the previous mentioned, again puts one ball in each of the arbitrary chosen four boxes. The probability that there are balls in at least 6 boxes is
Sir pls solve
Asked By: KANDUKURI ASHISH
is this question helpfull: 1 0
submit your answer
Joshi sir comment

Between two numbers, whose sum is 13/6, an even number of arithmetic means are inserted, the sum of these means exceed their number by unity. How many means are there?
Asked By: PREM
is this question helpfull: 2 0
submit your answer
Joshi sir comment

If 9a+24b=1, a,b, ∈ℝ+, prove that a2+b2≥ 9( 4+3√9)3.
Asked By: JAMES GHOSH
Joshi sir comment


Asked By: ASHLOK
is this question helpfull: 2 1
submit your answer
Joshi sir comment
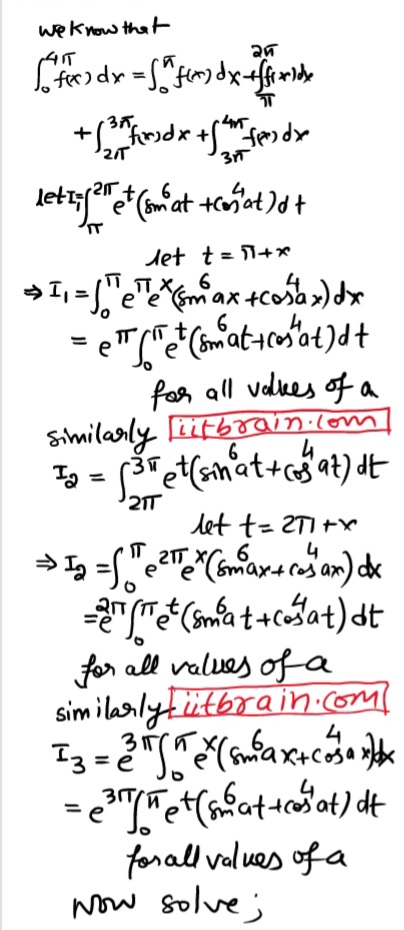
The expression ax2
+ 2bx + b has same sign as
that of b for every real x, then the roots of equation
bx2
+ (b – c) x + b – c – a = 0 are
(A) real and equal (B) real and unequal
(C) imaginary (D) None of these
Asked By: PREM
is this question helpfull: 1 0
submit your answer
Joshi sir comment

If a,b and c are positive real numbers, show that
ab+c+bc+a+ca+b≥32
Asked By: MROY
Joshi sir comment

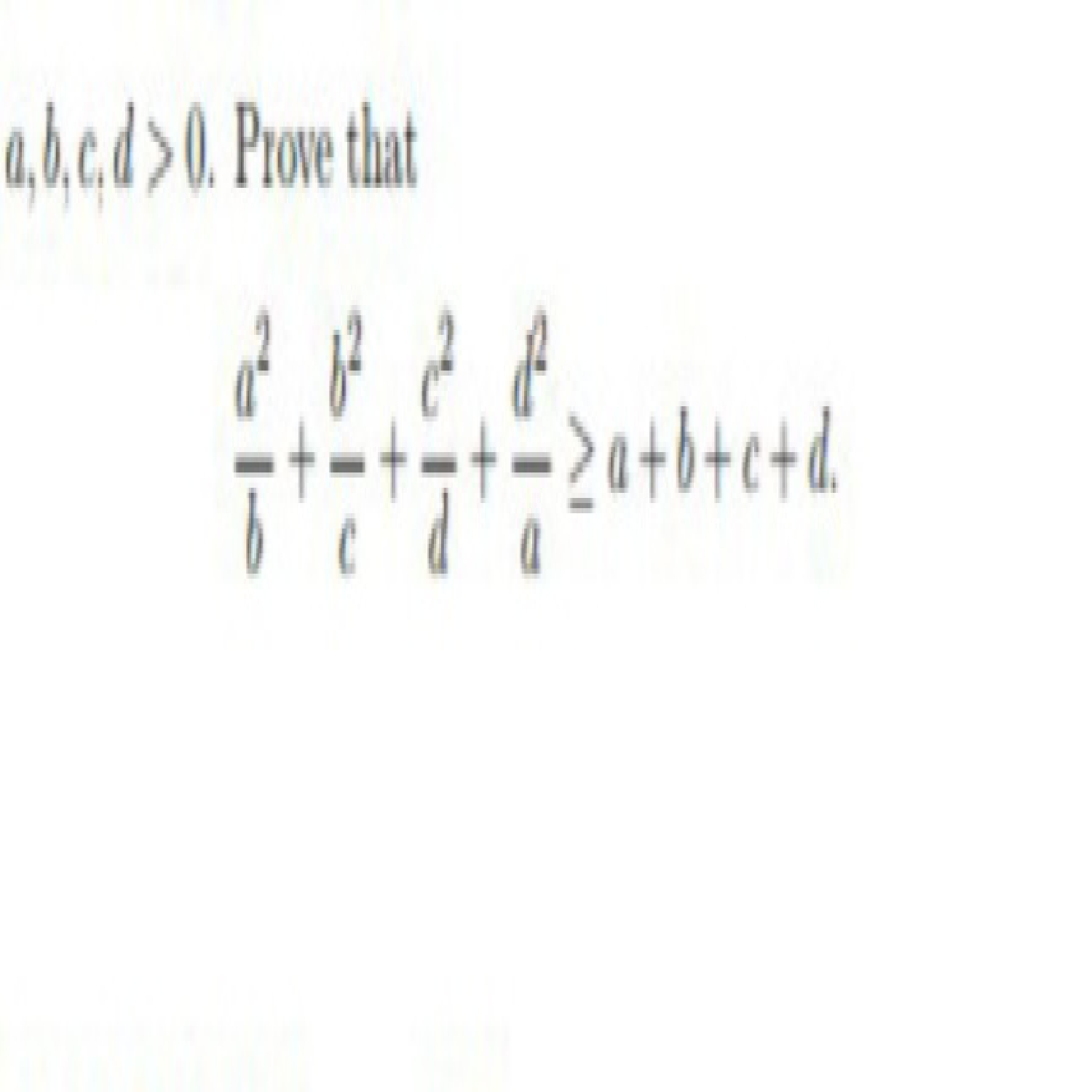
Asked By: LUFFY
is this question helpfull: 0 0
submit your answer
Joshi sir comment


.png)


