5 - Matrices and Determinants Questions Answers

first use C1 = C1+C2+C3

then R1 = R1+R2 and R2 = R2+R3

after it solve mathematically

let the 4 digit number is 1000a+100b+10c+d

then according to the given condition b=3a, c=a+b, d=2b

so c=4a, d=6a and b=3a

on putting all the values we get number = 1000a+100(3a)+10(4a)+6a = 1346a

on putting a =1, number = 1346

rank(A) = 1 
det(A) = 0 
trace(A) = 0 
The matrix is not symmetric. 

characteristic polynomial of the given matrix is x³ 

companion matrix of the polynomial (x+1)²

 0     1

-1    -2

A real symmetric matrix of rank r is congruent over the field of real numbers to a canonical matrix

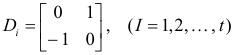
The integer p is called the index of the matrix and s = p - (r - p) is called the signature.

The index of a symmetric or Hermitian matrix is the number of positive elements when it is transformed to a diagonal matrix. The signature is the number of positive terms diminished by the number of negative terms and the total number of nonzero terms is the rank.

now solve it

Left hand derivative of given function at x = k (k is an integer) is

   lim_{h -> 0} {f(k-h) - f(k)}/ {k-h-k}  

= lim_{h -> 0} {[k-h] sin π(k-h) - [k] sin πk}/{-h}                  now 2 cases arise for even and odd k

first case

= lim_{h ->0}  (k-1) sin (-πh) - 0 / (-h)                          if k is even ,   here we used sin πk = 0 and sin (2π-x) = sin (-x) 

= π(k-1)                   here we used sin (-πx)/(-πx) = 1

second case

= lim_h->0 (k-1) sin (πh) - 0 / (-h)                            if k is odd,    here we used sin πk = 0 and sin (3π-x) = sin x

= -π(k-1) 

Left hand derivative of given function at x = k (k is an integer) is

   lim_{h -> 0} {f(k-h) - f(k)}/ {k-h-k}  

= lim_{h -> 0} {[k-h] sin π(k-h) - [k] sin πk}/{-h}                  now 2 cases arise for even and odd k

first case

= lim_{h ->0}  (k-1) sin (-πh) - 0 / (-h)                          if k is even ,   here we used sin πk = 0 and sin (2π-x) = sin (-x) 

= π(k-1)                   here we used sin (-πx)/(-πx) = 1

second case

= lim_h->0 (k-1) sin (πh) - 0 / (-h)                            if k is odd,    here we used sin πk = 0 and sin (3π-x) = sin x

= -π(k-1) 

so for even and odd k answer will be different.

I think the right question is  

f(x)  = ₀∫^x ( t²-t+2 )²⁰⁰⁵( t²-t-2 )²⁰⁰⁷( t²-t-6 )²⁰⁰⁹( t²-t-12 )²⁰¹¹( t²-3t+2 )²⁰¹²  dt    

then sum of values of x,  where maxima of f(x) will be obtained is

for maxima f '(x) = 0

by using Newton Lebnitz formula we get

f ^'(x) =  (x²-x+2 )²⁰⁰⁵( x²-x-2 )²⁰⁰⁷( x²-x-6 )²⁰⁰⁹( x²-x-12 )²⁰¹¹( x²-3x+2 )²⁰¹²

comparing it with 0 and making factors we will get x = -1, 2, 3, -2, 4, -3, 1

now obtain the maxima point then sum these values