33 - Trigonometry Questions Answers
If [cot‾1x] + [cos‾1x] = 0 , then complete set of value of x is ( [ * ] is GIF)?

These are the graphs for cot-1x and cos-1x
violet for cos and green for cot
from graph it is clear that cos part with integer function will be 0 for cos1<x≤1
and cot part with integer function will be 0 for cot1<x<∞
so answer will be cot1<x≤1
A regular hexagon and a regular dodecagon are inscribed in the same circle. if the side of the dodecagon is (√3-1), then the side of hexagon is
for dodecagon sin(2π/40) = (a/2)/r so r = (a/2)/ sin(π/20)
now for hexagon sin(2π/12) = (x/2)/r so x/2 = r sin(π/6) = (a/2) sin(π/6)/ sin(π/20)
so x = (√3-1) (1/2) / ((√5-1)/4) here sin(π/20) = (√5-1)/4
or x = 4(√3-1) / 2(√5-1)
now solve it for further simplification
What are trigonometrical identities?
sin2A + cos2A = 1 and two similar formulae in terms of tanA, cotA, secA and cosecA
these are identities because these are true for all values of A
if secA-tanA=3
then find the value of (5cosA+4cotB)??
jus a hint
First replace cotB by cotA.
because it is wrongly printed by you.
answer by NIKHIL is correct
Which of the following angles are co-terminal angles: 480 , -240 or 600
how can we get it which is co-terminal and what does co-terminal means?????
Coterminal angles are angles in standard position (angles with the initial side on the positive x-axis) that have a common terminal side. For example 30°, –330° and 390° are all coterminal.
To find a positive and a negative angle coterminal with a given angle, you can add and subtract 360° if the angle is measured in degrees or 2π if the angle is measured in radians.
480 and -240 are co terminal angles because 480-360 = 120 and -240+360 = 120

is there any need to know or learn the proof pf formulas of trigo
No, For making a good command in trigonometry, only implementation is a need. But for your knowledge you can proof these results
if x,y,z are acute and cos x= tan y , cos y = tanz , cos z = tan x, then the value of sin x is ;
by 1st equation sec y = √(1+cos2x) so cos y = 1/ √(1+ cos2x)
by 3rd equation sec z = cot x so tan z = √(cot2x - 1)
on putting these 2 values in 2nd equation we get
1/ √(1+ cos2x) = √(cot2x - 1)
so sin2x = (1+cos2x)(cos2x-sin2x)
or sin2x = (2-sin2x)(1-2sin2x)
or sin2x = 2-4sin2x-sin2x+2sin4x
or 2sin4x-6sin2x+2 = 0
now solve it for sinx
If a sinx + b cos(x+θ) + b cos(x-θ) = d, then the minimum value of |cos θ| is equal to :
sir i have expanded cos(x+θ) & cos(x-θ) and after that i got the equation: (d sec x - a tanx)/2b = cos θ. now , can i write minimum value of (d sec x -a tanx) = (d²-a²)^(1/2).. as all the options contain (d²-a²)^(1/2).......or do tell the other hint to solve it..
Dear amit your starting steps are correct
now let us consider that d secx - a tanx = y
on differentiating we will get d secx tanx - a sec2x = dy/dx
on comparing with 0 we get d tanx = a secx or sinx = a/d so secx = d/√(d2-a2) and tanx = a/√(d2-a2)
so minimum of given expression = [d2/ √(d2-a2)] - [a2/√(d2-a2)] = √(d2-a2)
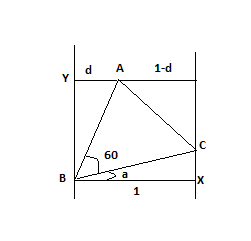
The distance between two parallel lines is 1.A point 'A' is chosen to lie between the lines at a distance 'd' from the first line. Triangle ABC is an eqilateral triangle with 'B" on one line and 'C' on the other line.Then AB is equal to(in terms of d).
In triangle BCX
BC = seca
so AB = seca
now in triangle ABY
cos(60+a) = d/seca
so 1/2 cosa - √3/2 sina = d cosa
or tana = (1-2d)/√3
now calculate seca
let z be a complex number satisfying |z-3|=|z-4i|, then find the least possible value of 10|z|.
In |z-3|=|z-4i|, z represents all points lying on the perpendicular bisector of the line joining 3 and 4i in x-y plane. In this perpendicular bisector, if we draw a perpendicular then it will be the minimum magnitude of z. Construct this as a diagram we will get
sinθ = |z| / (7/8)
or |z| = (7/8)(4/5) = 7/10

