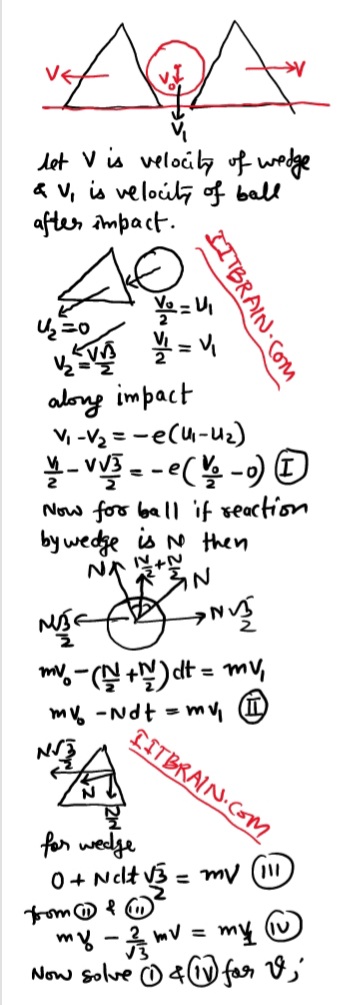
11 - Centre of mass and momentum conservation Questions Answers
In a gravity free space a small ball is placed at the centre of a box of the same mass. The ball and the box both are moving with velocity u towards a fixed wall. Assume all collisions are perfectly elastic.
A) How many collisions are possible?
B) find velocities of the box and the ball and the position of the ball relative to the box after all possible collisions.

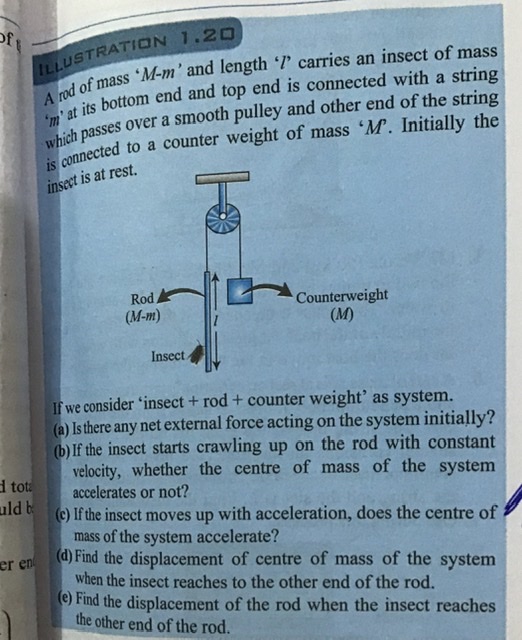
Updated:
Initially there is no external force. Centre of mass of the system accelerates when insect moves with acceleration.
Now suppose displacement of insect at t = t is x with respect to rod, and y is the acceleration of rod in downward direction with respect to ground. Thus acceleration of counterweight is y with respect to ground. NowNow solve for x = l,
For dynamics, take friction upward in free body diagram of insect and downward in the free body diagram of rod.

Now solve
Inform for any issue.
distance covered in n sec. = un+an2/2 (1)
distance covered in n-1 sec. = u(n-1)+a(n-1)2/2 (2)
so sn = (1) - (2)
put equation (1) and (2) and get the answer
the moment of inertia of a thin uniform rod about an axis through its end and perpendicular to its length is ML²/3 . The moment of inertia of the rod about an axis parallel to given axis and at a distance L from the center of the rod is
for an axis parellel to the axis of rod and at distance l, rod will act as a set of equidistance particles. so answer will be Ml2
answer given by sarika is not completely correct
velocity of impact = √2gh
so components of velocity after rebound = √2ghcosθ perpendicular to the plane and √2ghsinθ parallel to the plane for the collision is perfectly elestic
now with perpendicular component take net displacement 0 and calculate time
then find displacement along the plane by using s = ut + 1/2at2
here remember that you should divide gravity in comnents too


.png)