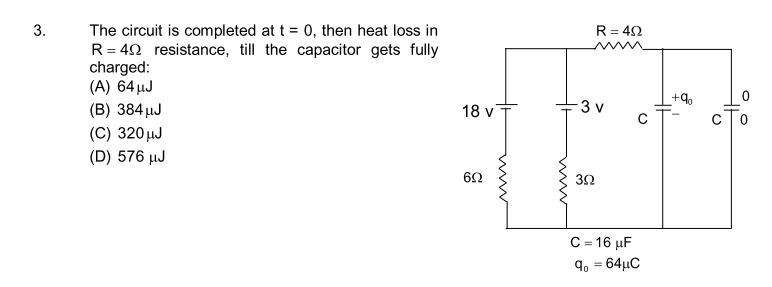
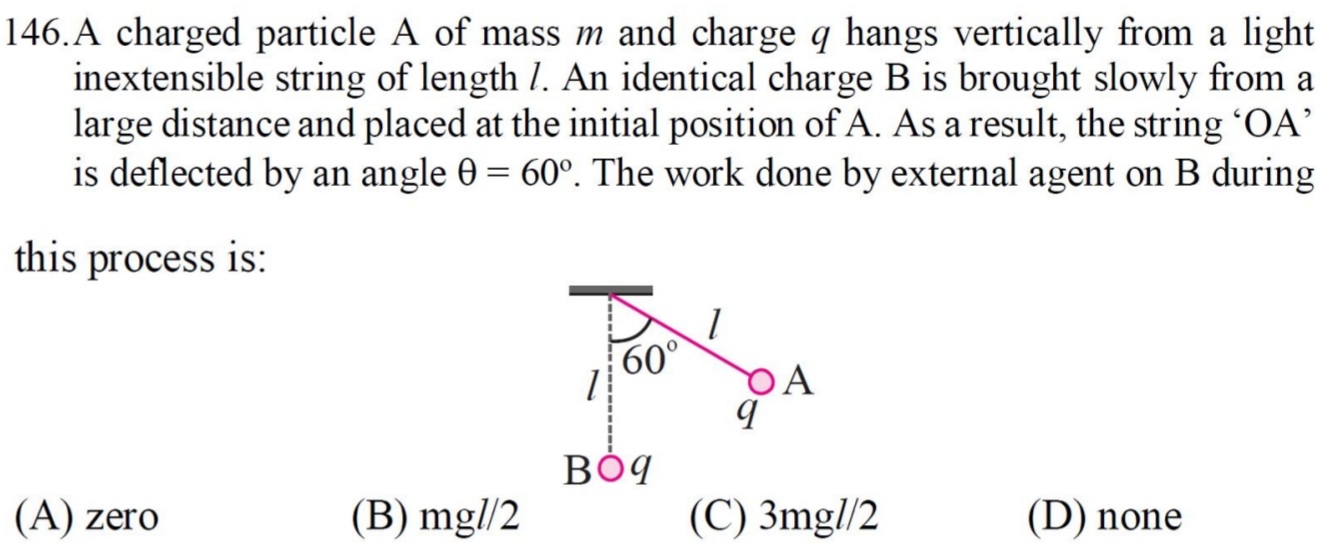
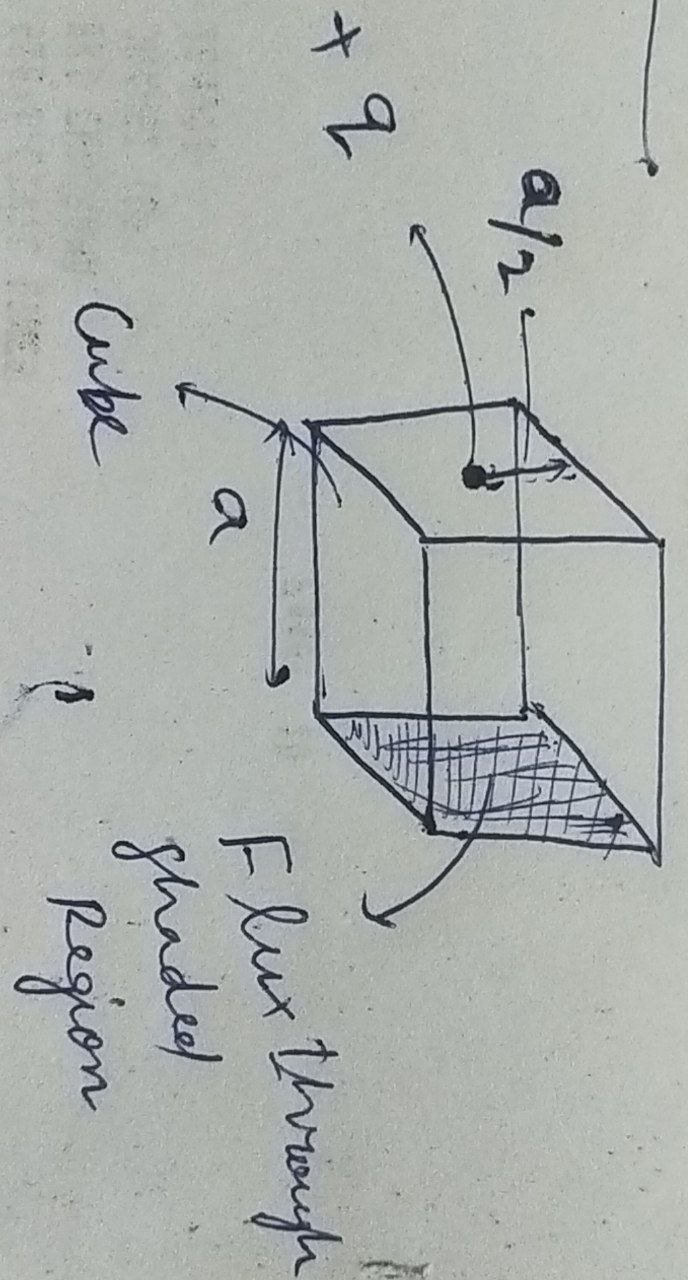
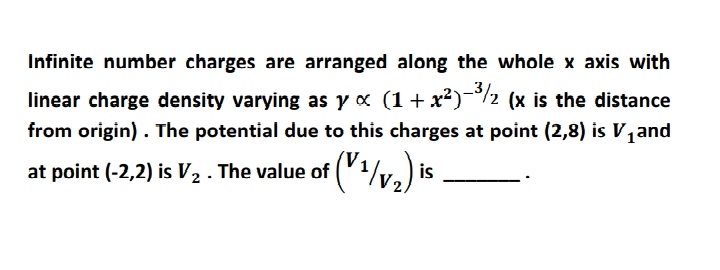87 - Electricity Questions Answers
Please explain krotov questions 3.26 of electricity
Asked By: RITESH KUMAR
is this question helpfull: 2 0
submit your answer
A uniform electric field is established by connecting the plates of a parallel plate capacitor to a 12v battery. A charge particle of +6.24x10 to the power -6c moves from rest from the positive plate to the negative plate. when the charge reaches the negative plate,it acquires a speed of 3.4m/s.what is{a} the mass of the charge particle and{b} its final kinectic energy?
Asked By: GIRISH
is this question helpfull: 0 0
submit your answer
Asked By: TAPASGUPTA
An electric dipole moment p=(i-3j+2k)10^-29 Cm is at origin (0,0,0).The electric field due to this dipole at r=i+3j+5k (note p.r≠0) is parallel to ?
Asked By: PRIYANSHU SINGH
is this question helpfull: 1 1
submit your answer
E= 2x/(x²+y2 ) i + 2y/(x²+y²) j
V find karna hai
Asked By: RAJAT SINGH
is this question helpfull: 1 0
submit your answer
Asked By: AYUSH KAUSHIK
is this question helpfull: 0 0
submit your answer
