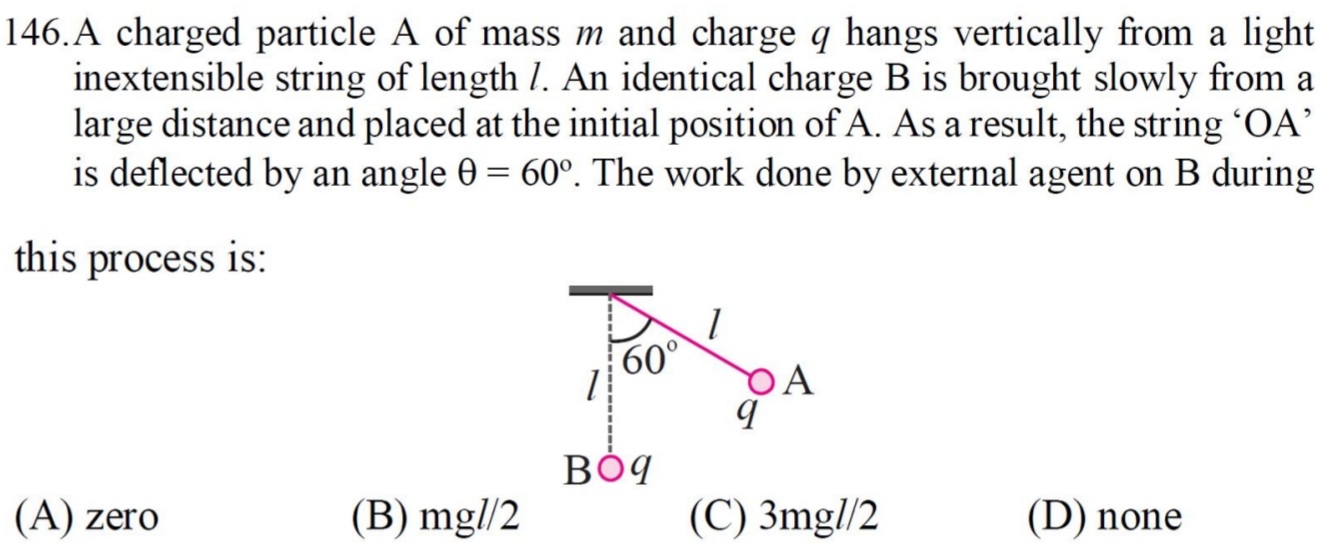
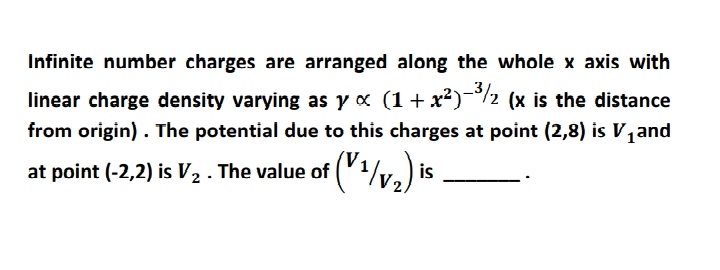51 - Electric Field and Potential Questions Answers
A small ball of mass 1kg and charge 2 C 3 is placed at the centre of a uniformly charged sphere of radius 1m and charge 1mC 3 . A narrow smooth groove is made in the sphere from centre to surface as shown in figure. The sphere is made to rotate about its vertical diameter at a constant rate of 1 2 revolutions per second. Find the speed w.r.t. ground with which the ball slides out from the groove. Neglect any magnetic force acting on ball
A uniform electric field is established by connecting the plates of a parallel plate capacitor to a 12v battery. A charge particle of +6.24x10 to the power -6c moves from rest from the positive plate to the negative plate. when the charge reaches the negative plate,it acquires a speed of 3.4m/s.what is{a} the mass of the charge particle and{b} its final kinectic energy?
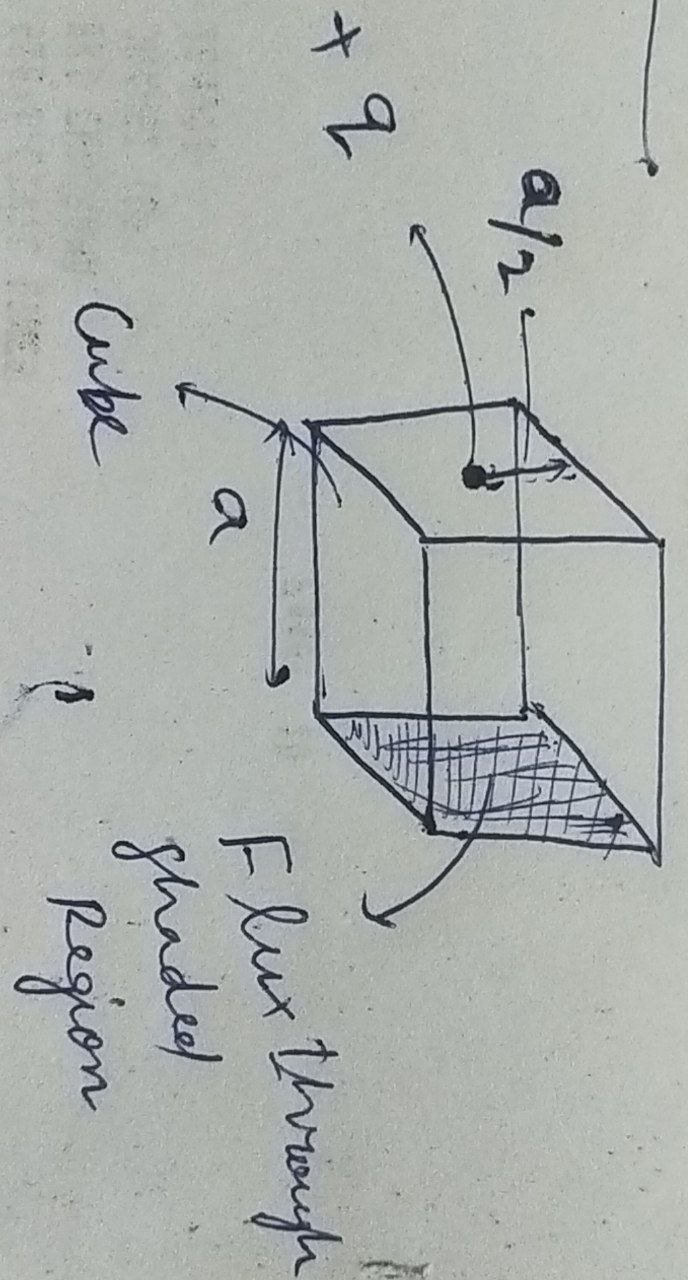
An electric dipole moment p=(i-3j+2k)10^-29 Cm is at origin (0,0,0).The electric field due to this dipole at r=i+3j+5k (note p.r≠0) is parallel to ?
E= 2x/(x²+y2 ) i + 2y/(x²+y²) j
V find karna hai
. Dear Sir kindly help solve this question