7 - Fluid in motion Questions Answers
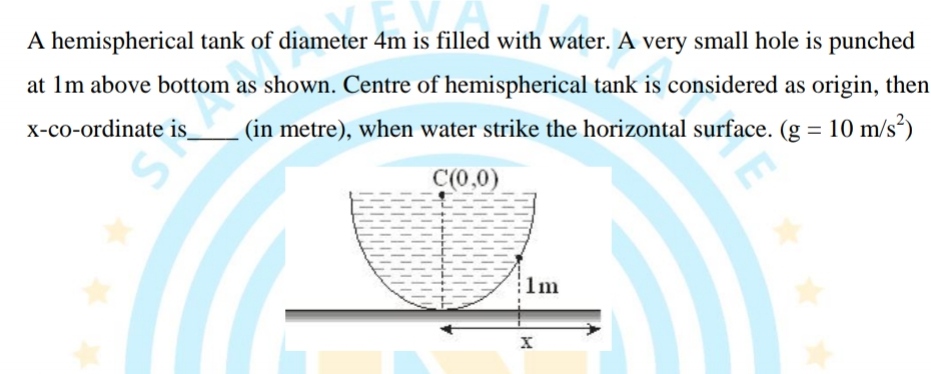
By Bernoullis theorem, velocity of water jet = √2ghWater jet comes out perpendicular to surface.
make its horizontal and vertical components
By vertical component, calculate time, then use it with
horizontal velocity component to get distance along x axis
Finally calculate distance from centre, along x axis
Inform for any confusion


can the linear speed of two objects be different if they have the same angular speed?
angular speed depends on the distance from pivot also so v may be same or different
formula affilated is v = r ω
THE TERMINAL SPEED ATTAINED BY AN Al SPERE OF RADIUS 1mm FALLING THROUGH H2O AT 200C WILL BE CLOSE TO ??
ANS 4.6 m/s
(assume laminar flow , specific gravity of Al=2.7 & η H2O =8X 10-4 PL.)
v = 2r2g(D-d)/9η
so v = 2(.001)2*9.8(2700-1000)/9*8*10-5
solve it
Q IF IN THE SAME QUESTn OF BAROMETER THE ELEVATOR IS ACCELERATING UPWARD READS 76cm. THEN AIR PRESSURE IN ELEVATOR IS >76cm PLS EXPLAIN THE CONCEPT BEHIND SUCH CASES.
when elevator will move in upward direction the extra Hg level will feel a down force and given that in movable condition it is 76 cm. Hg so really it will be more than 76 cm.
There is some amount of water in the beaker, and a vertical rod is passing through the centre of the circular base of the cylindrical beaker which is rotated with angular velocity ω , then water takes a particular shape(miniscus is formed). Find the equation of the miniscus of water when the mid point of the miniscus just touches the bottom surface of the beaker?
after making the diagram, complete the miniscus as a sphere, then following conditions will be obtained
1) h = R(1-cosθ) here h, R and θ are height of miniscus, radius of the sphere and contact angle.
2) R = r/cosθ, r is the radius of beaker
3) tanθ = g/rw2
4) πr2hρ - πR3ρcos2θ = 2πrTcosθ
There are 4 equations, remove R, θ and T and get a relation between h and r in terms of g, w, ρ and π
