302 - Mechanics part 1 Questions Answers
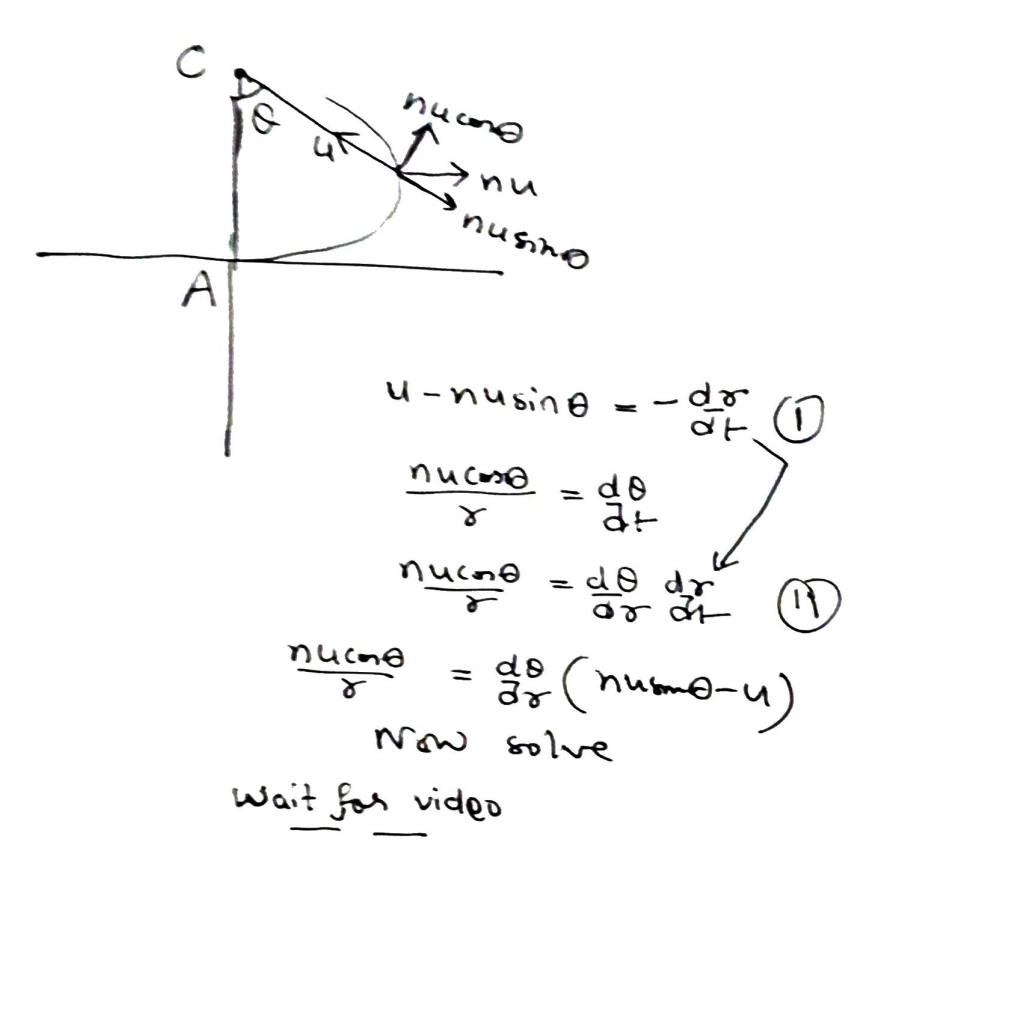
A rotating ball hits a rough horizontal plane with a vertical velocity and angular velocity . Given that the coefficient of friction is and the vertical component of the velocity after the collision is , find:
a) the angular velocity after collision;
b) the impulsive ground reaction during the collision
on applying momentum impulse theorem along vertical
-mv+Ndt = mv/2 (1)
by angular momentum angular impulse theorem
By eq. (2) get angular velocity.
impulsive ground reaction = by using eq. (1), solve it
Hi please slove these question also...
A ) Two particles of mass 3 kg and 4 kg are connected by a light inelastic string passing over a smooth fixed pulley. The system is released from rest with the string taut and both particles at a height of 2 m above the ground. Find the velocity of the 3 kg mass when the 4 kg mass reaches the ground, and find when the 4 kg mass reaches the ground.
B) Briefly describe an experiment to find the coefficient of friction between brick and tile. You may assume access to a tile slab, a number of bricks and basic scientific equipment, such as a pulley, weighing machine, etc.
Please reply ASAP...Waiting for your reply.
(A)4g-T = 4a
T-3g = 3a
solve for a
use h = 0t+1/2at2 for getting t
and v = 0 +at for v
(B) get F applied and acceleration of the body
then use F-kmg = ma
for getting k (coefficient of friction)
Please slove the below mention question:
A) A uniform ladder of weight w rests on rough horizontal ground against a smooth vertical wall. The vertical plane containing the ladder is perpendicular to the wall and the ladder is inclined at an angle θ to the vertical. Prove that, if the ladder is on the point of slipping and µ is the coefficient of friction between it and the ground, then tanθ = 2µ
B) Two particles of mass 3 kg and 4 kg are connected by a light inelastic string passing over a smooth fixed pulley. The system is released from rest with the string taut and both particles at a height of 2 m above the ground. Find the velocity of the 3 kg mass when the 4 kg mass reaches the ground, and find when the 4 kg mass reaches the ground.
C) A box of mass 14 kg is placed in the back of a van. The coefficient of friction between the box and the floor is 0.5. What happens to the box if the lorry moves off with an acceleration of
(a) 4 ms-2
(b) 5 ms-2
(c) 8 ms-2
(Take g = 10 ms-2)
Can i get answer before 3pm today. Please i request you to help me out from the issue...
(a)let R and N are reactions by the ground and wall then for equilibrium
μR = N
R = w
and about ground point
N*lcosθ = w*lsinθ/2
now solve
(b) 4g-T = 4a
T-3g = 3a
solve for a
use h = 0t+1/2at2 for getting t
and v = 0 +at for v
(c) for a = 8 pseudo force = 14*8 and friction max = 0.5*14*10 so box will fall in backward direction
A 50 kg gymnast falls freely from a height of 4 m on to a trampoline. The trampoline then bounces her back upward with a speed equal to the speed at which she first struck the trampoline. What is the average force the trampoline applies on the gymnast ?
A) 50 N B) 200 N C) 500 N D) 2000 N E) more information is required
rain is falling down vertically 2m/s. a person is walking with velocity 2m/s on horizantal road. the angle made by the umbrella with vertical to protect from rain is
a block of mass m is pushed up a movable incline of mass nm and height h.All surfaces are smooth without friction.what must be the minimum value of u so that the block just reaches the top of the movable incline.
let velocity of m at start is u along horizontal
at the top horizontal velocity of system = u/(n+1) and vertical velocity = 0
by energy conservation 1/2 mu2 = 1/2 (nm+m) {u/(n+1)}2 + mgh
solve
a package of mass 10kg is released from rest on a rough slope inclined at 25 degrees to the horizontal. after 2 seconds the package has moved 4m down the slope. find the coefficient of friction between the package and the slope.
a box of mass 2kg is pushed up a rough plane by a horizontal force of magnitude 25N. the plane is inclined to the horizontal at an angle of 10 degree. given that the coefficient of friction between the box and the plane is 0.3, find the acceleration of the box.
first part is correctly explained by Sarika
for second part make components of forces as 25 N and weight along and perpendicular to the incline, friction μN will be along downward incline and N will be the resultant of components of weight and 25 N perpendicular to the plane.
In order to raise a mass of 100 kg, a man of mass 60 kg fastens a rope to it and passes the rope over a smooth pulley. He climbes the rope with an acceleration 5g/4 relative to the rope. The tension of the rope is:
(a) 1432 N
(b) 928 N
(c) 1218 N
(d) 642 N
eq. for upward motion of 100 Kg is T-100g = 100a (1)
for man eq. is T-60g = 60[(5g/4)-a] from ground frame
solve?