89 - Electricity Questions Answers

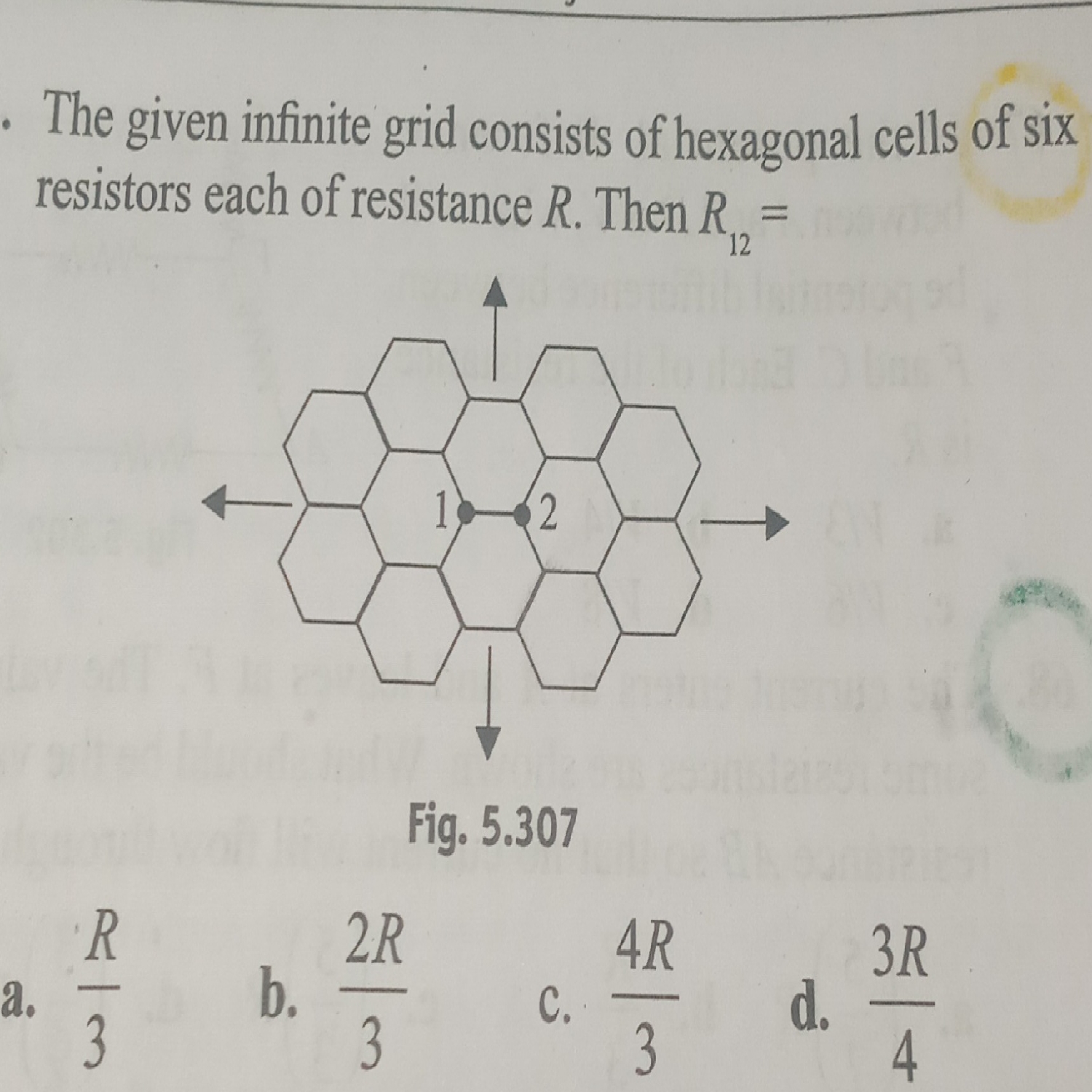
By superposition principle, it is solved in minimum time and effort, other method is very complex. So use superposition principle.

Divide current in point 1 and 2, considering symmetry throughout, we get the equivalent resistance of the whole network except resistor R between 1 and 2 is 2R

Now 2R and R in parallel between 1 and 2

Now solve

$$\begin{gathered} Potential difference from centre to surface = 3V/2 - V = V/2 \\ here V = kq/r (q is charge of sphere) \\ m{v_r}^2/2 = VQ/2 (Q is charge of particle) \\ {v}_r is radial velocity \\ Besides \tan gential velocity due to rotation of sphere = r\omega =r2\pi n \\ now solve \end{gathered}$$

$$\begin{gathered} By volume comparision radius of combined drop = 2^{1/3}r \\ net charge in the new drop = 2q \\ now put these values in the formula of potential \end{gathered}$$

No meaning can be incurred by this language. Rectify it for getting answer

$$\begin{gathered} Since thickness is same so force per unit length should be same \\ Force per unit length = F/2\pi R \\ Charge density in the sphere is proportional to E \\ so F \alpha qE \alpha \sigma AE \alpha E^2{R}^2 \\ Thus force per unit length \alpha E^2{R}^2/2\pi R \alpha E^{2}R \\ Now compare the two cases \end{gathered}$$

$$\begin{gathered} \frac{k{q}_1{q}_2}{{l_3}^2}=\frac{k{q}_2{q}_3}{{l_1}^2}=\frac{k{q}_3{q}_1}{{l_2}^2} \\ {l}_1+l_2+l_3=L \\ from these 2 equations \\ \frac{L \frac{1}{\sqrt{q_1}}}{\frac{1}{\sqrt{q_1}}+\frac{1}{\sqrt{q_2}}+\frac{1}{\sqrt{q_3}}},\frac{L \frac{1}{\sqrt{q_2}}}{\frac{1}{\sqrt{q_1}}+\frac{1}{\sqrt{q_2}}+\frac{1}{\sqrt{q_3}}},\frac{L \frac{1}{\sqrt{q_3}}}{\frac{1}{\sqrt{q_1}}+\frac{1}{\sqrt{q_2}}+\frac{1}{\sqrt{q_3}}} \end{gathered}$$

area = l²/2 = 8 so l = 4

ρ = 1 

so  resistance of the 3 legs of the triangle = 4/A, 4/A, 4√2/A

battery is connected across the longest branch so eq. resistance = 4/A+4/A+4√2/A = 13.6/A

i think area of cross section will be given then calculate current

use kirchhoff laws

4-10i+1-30x = 0

1-30x+20(i-x) = 0

solve it for i and x

potential across A and B = 4-10i+1 = 30x

since the circuit is symmetrical with respect to the line given so V, the potentials at the given points will be same 

now calculate the eq. for the half circuit and double it for getting the eq. of the whole circuit

since the circuit is symmetrical with respect to the line given so V, the potentials at the given points will be same 

now calculate the eq. for the half circuit and double it for getting the eq. of the whole circuit

for one side eq. of 2 and 4 = 4/3

and then 4 in series of it so 4/3 + 4 = 16/3

finally 16/3||4/3 

eq = 16/15

final answer = 16/15 * 2 = 32/15