71 - Newton's laws of motion and friction Questions Answers
Irodov 1.2 Q61
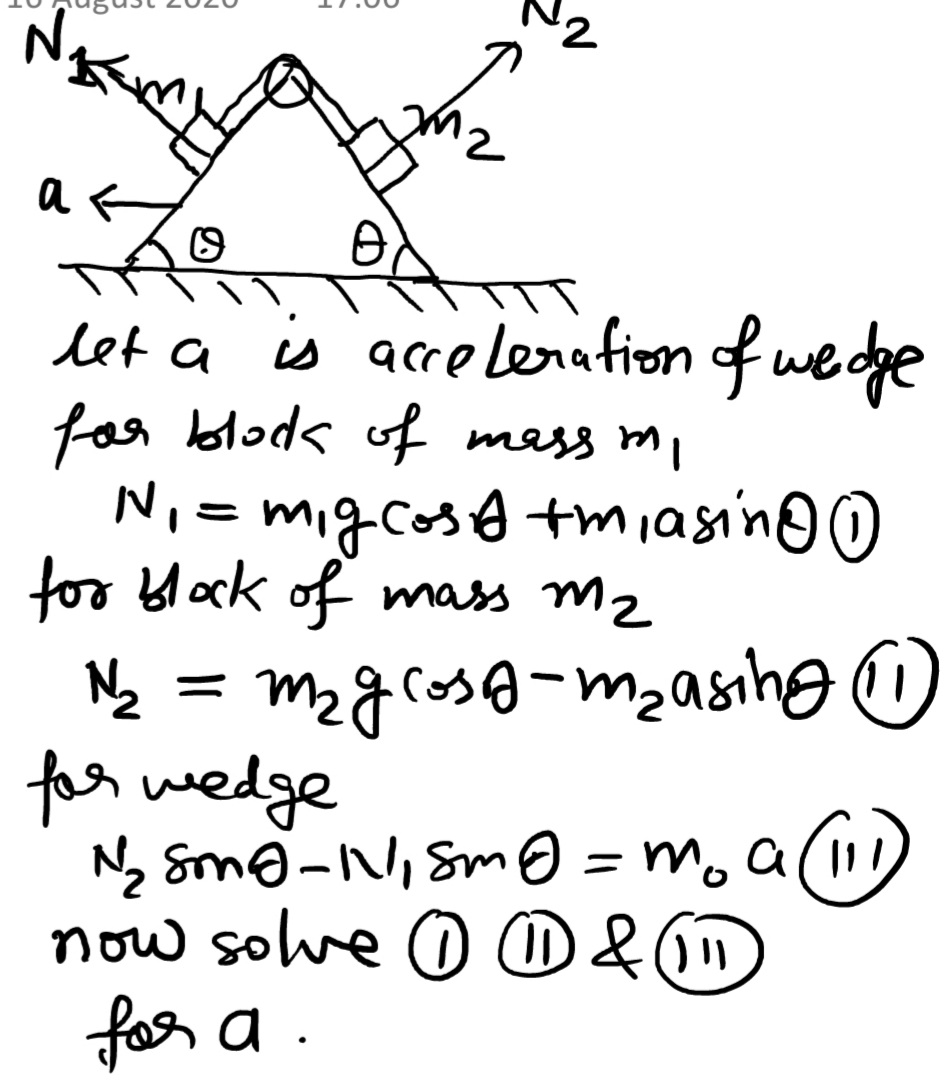
two touching bars 1 and 2 are placed inclined plane forming an angle alpha with horizontal the masses of the bars are equal to M1 and M2 and the coefficient of friction between the inclined plane and these bars are equal to K1K2 respectively with the k1>k2 . find
a) the force of interaction of the bars in the process of motion
b) the minimum value of the angle alpha at which the bars start sliding down
my doubt;
if I consider them to be 1 mass system , then what would happen to the resultant friction coefficient of the 1 mass system , would it be k1 + k2 ?
thank you
Why do you want to consider this, I do not know, yet if you consider them as a body and make free body diagram then apply friction on the two blocks separately, in one it depends on k1 and in second it depends on k2. No concept of k1 + k2 is there in physics
_LI_3.jpg)
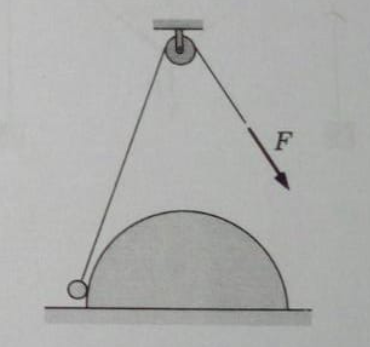
A small metal ball is being pulled gradually on a fixed frictionless hemisphere as shown in the figure. Radii of the ball and that of the pulley are much smaller than that of the hemisphere. As the ball slides from the bottom to a position close to the top of the hemisphere, how do the magnitudes of pulling force F and contact force R between the ball and the hemisphere change?
(a) F increases and R decreases.
(b) F decreases and R increases.
(c) F decreases and R remains unchanged.
(d) F remains unchanged and R decreases.
Three identical balls are placed on a frictionless horizontal surface touching each other. They stick to each other because of adhesive. Another ball of same radius and mass m is placed on the void created by the three balls. Find the forces applied by the balls kept on the floor to each other if the system remains in equillibrium.
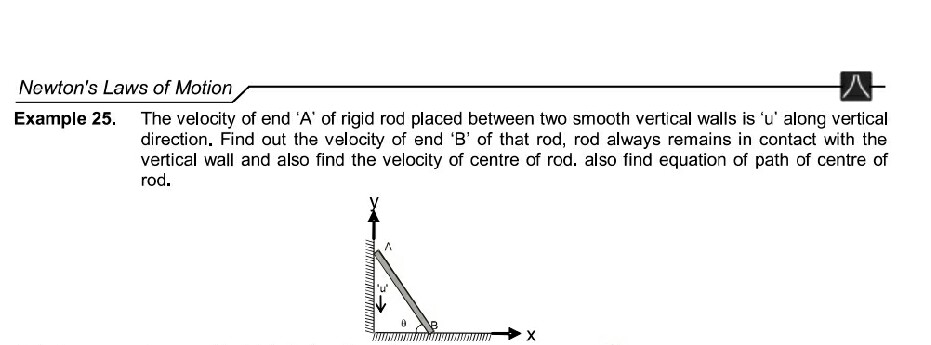
By rigid body constraints
Use formula F(min)/mg = mg/F(max)
Now solve. Watch this video
A particle of mass m = 2kg is placed on the top of a hemisphere of M 4 kg. The hemisphere is placed on smooth ground. The particle is displaced gently. Then ratio of normal and pseudo force(seen from hemisphere frame) acting on particle when theta = 30 degree. Assume particle remain in contact with hemisphere.
