576 - Physics Questions Answers

Current comes out from the surface of one sphere symmetrically 

and enters to the surface of other symmetrically.

Resistance of the medium around one sphere is

$$\begin{gathered} {\int }_r^{\infty }\frac{\rho dx}{4\pi x^2}=\frac{\rho }{4\pi }\left[-\frac{1}{x}\right] \\ on putting limits resis\tan ce around \\ one sphere =k\frac{1}{r} \\ similar for other sphere so net R_1=2\frac{k}{r} \\ In second case radius of one sphere \\ is half means r/2 \\ Thus R_2 = \frac{k}{r}+\frac{k}{r/2}=3\frac{k}{r} \\ now for same battery i_1{R}_1=i_2{R}_2 \\ solve and wait for video \end{gathered}$$ 

At the front of the cylinder, see a tilted circle $$\begin{gathered} Now compare this problem with vertical circular motion. \\ A is the top point of that path. We know that the \\ minimum velocity at top point \tan gential to path of \\ vertical circle should be \sqrt{gr}. \\ Here due to tilt of this circle effective gravity = g\cos \alpha \\ so v\sin \phi =\sqrt{g\cos \alpha r} \\ now solve \\ inform for any issue \\ wait for video \end{gathered}$$

According to first given condition velocity component of rain = u

let vertical component of rain = v

According to second condition 

velocity of rain relative to man 

$=(nu-u)(-\hat{i})+v(-\hat{j})$$$\begin{gathered} here direction of motion of man is \hat{i} and \\ vertically upward direction is considered as \hat{j} \\ Now draw triangle for this vector and get cot\theta \\ solve it \\ inform for any issue \end{gathered}$$

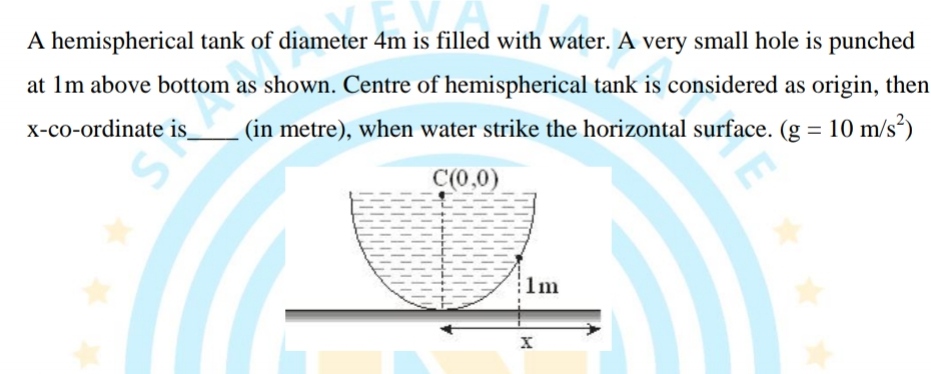
By Bernoullis theorem, velocity of water jet = $\sqrt{2gh}$Water jet comes out perpendicular to surface.

 make its horizontal and vertical components

By vertical component, calculate time, then use it with 

horizontal velocity component to get distance along x axis

Finally calculate distance from centre, along x axis 

Inform for any confusion

Updated:

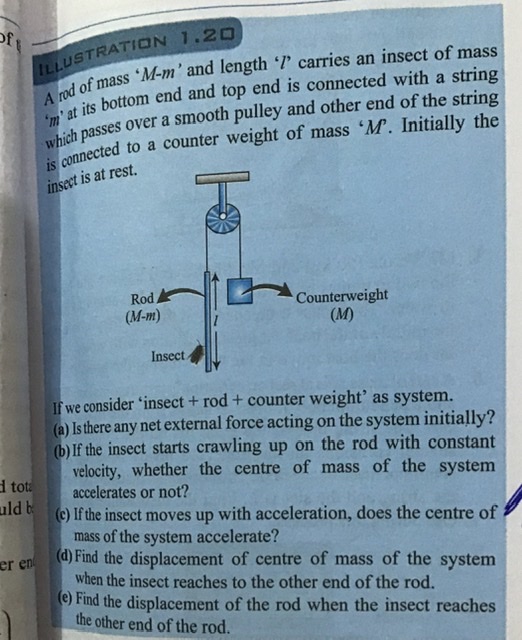
Initially there is no external force. Centre of mass of the system accelerates when insect moves with acceleration.

Now suppose displacement of insect at t = t is x with respect to rod, and y is the acceleration of rod in downward direction with respect to ground. Thus acceleration of counterweight is y with respect to ground. Now$\overrightarrow{x_{CM}}=\left[m\right(x-y)\hat{j}-(M-m)y\hat{j}+My\hat{j}]/2M$Now solve for x = l,

For dynamics, take friction upward in free body diagram of insect and downward in the free body diagram of rod.

Now solve

Inform for any issue.

$$\begin{gathered} Let width=b \\ For nth state n\frac{\lambda }{2}=b \Rightarrow \lambda =\frac{2b}{n} \\ Now E =\frac{p^2}{2m} = \frac{{\left({\displaystyle \raisebox{1ex}{$h$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}\right)}^2}{2m} \\ Solve after putting the value of \lambda \\ Uncer\mathrm{ta}inty in position=b \\ Now use ∆p.∆x = nh/2\mathrm{\pi } \mathrm{for} \mathrm{finding} \mathrm{uncertainty} \mathrm{in} \mathrm{momentum} \end{gathered}$$

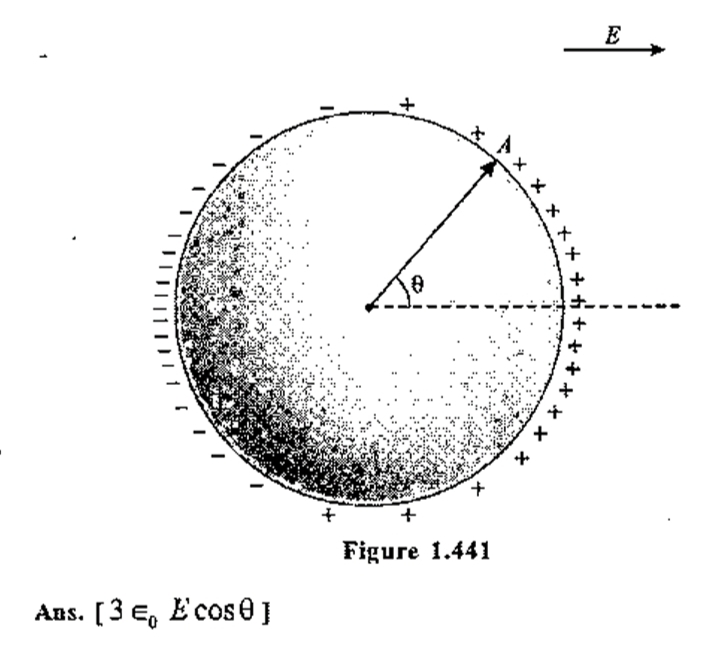
To nullify the electric field inside, the conducting sphere creates a situation in which electric field inside due to charge on sphere would be same as that of given electric field. Now this is the case, which is same as Irodov 3.17.

See the video now

link:

Finally$$\begin{gathered} E = \frac{{\sigma }_0}{3{\epsilon }_0} = \frac{\sigma }{3{\epsilon }_0\cos \theta } \\ Now solve \end{gathered}$$

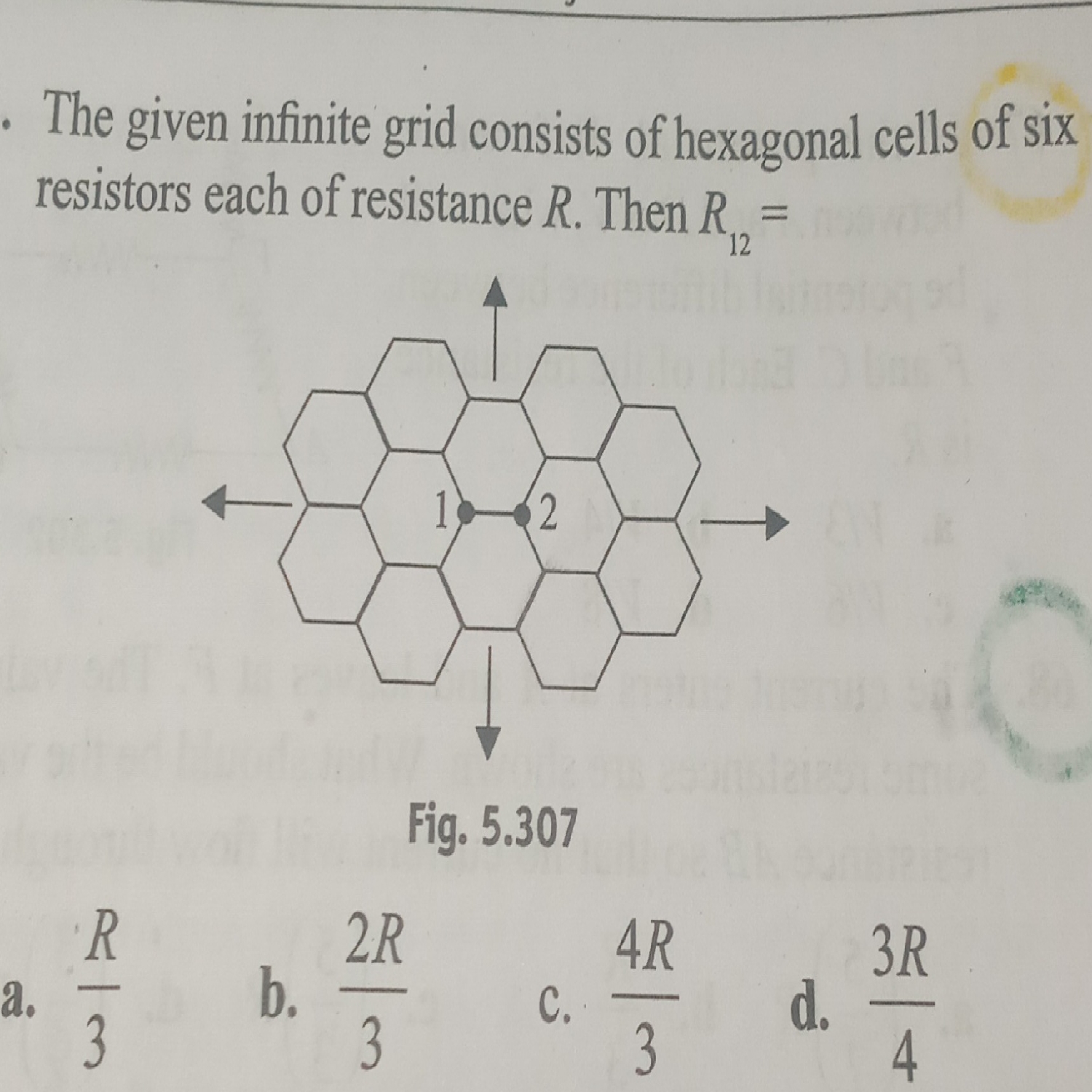
By superposition principle, it is solved in minimum time and effort, other method is very complex. So use superposition principle.

Divide current in point 1 and 2, considering symmetry throughout, we get the equivalent resistance of the whole network except resistor R between 1 and 2 is 2R

Now 2R and R in parallel between 1 and 2

Now solve

$$\begin{gathered} According to given condition 2r = {u_y}^2/2g, \\ T= 2u_y/g =2\sqrt{4gr}/g=4\sqrt{r/g} \\ At top point due to touch, vecocity of the frog be u_x-2v. \\ R=[u_x{u}_y/g]+[u_x-2v)u_y/g]=[u_y/g\left]\right(2u_x-2v) \\ =[2u_y/g\left]\right(u_x-v) =T(u_x-v) \\ Now minimum possible value of velocity of frog at top to \\ cross the cylinder is \sqrt{gr} (By the concept of vertical circle) \\ now solve carefully without error \end{gathered}$$