576 - Physics Questions Answers

Physics >> Optics >> Refraction IIT JEE

Asked By: BHASKAR JHA

is this question helpfull: 1 0 submit your answer

Joshi sir comment

$L e t α i s s m a l l a n g u l a r d i s p l a c e m e n t A s s h o w n x = l \sin α a n d y = l \cos α / μ n o w u s e \sin^{2} α + \cos^{2} α = 1$

Physics >> Mechanics part 1 >> Newton's laws of motion and friction IIT JEE

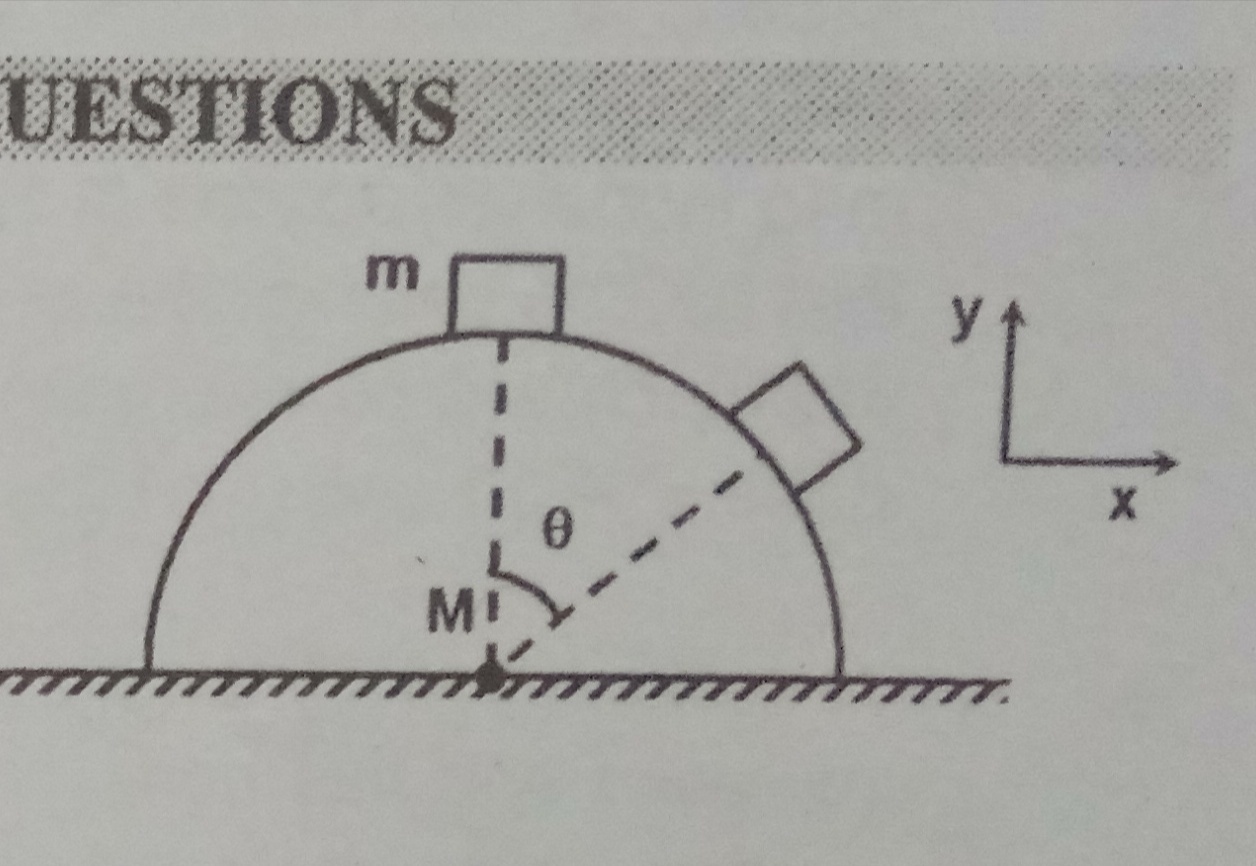
A particle of mass m = 2kg is placed on the top of a hemisphere of M 4 kg. The hemisphere is placed on smooth ground. The particle is displaced gently. Then ratio of normal and pseudo force(seen from hemisphere frame) acting on particle when theta = 30 degree. Assume particle remain in contact with hemisphere.

Asked By: GUDDU KUMAR

is this question helpfull: 2 0 submit your answer

Joshi sir comment

$L e t t h e a c c e l e r a t i o n o f h e m i s p h e r e i s a_{h} N \sin θ = M a_{h} \Rightarrow N / m a_{h} = M / m \sin θ H e r e p s e u d o f o r c e i s c o n s i d e r e d d u e t o a c c e l e r a t i o n o f h e m i s p h e r e$

Physics >> Electricity >> Electric Field and Potential IIT JEE

a small ball of mass 1kg and a charge 2/3 uC is placed at the center of a uniformly charged sphere of radius 1m and charge 1/3 mC. a narrow smooth horizontal groove is made in the sphere from centre to surface as shown in figure. the sphere is made to rotate about its vertical diameter at a constant rate of 1/2pi revolutions per second. find the spedd w.r.t ground with which the ball slide out from the groove. neglect any magnetic force acting on ball?

Asked By: VISHNU VARDHAN

is this question helpfull: 6 6 submit your answer

Joshi sir comment

$P o t e n t i a l d i f f e r e n c e f r o m c e n t r e t o s u r f a c e = 3 V / 2 - V = V / 2 h e r e V = k q / r (q i s c h a r g e o f s p h e r e) m {v_{r}}^{2} / 2 = V Q / 2 (Q i s c h a r g e o f p a r t i c l e) v_{r} i s r a d i a l v e l o c i t y B e s i d e s \tan g e n t i a l v e l o c i t y d u e t o r o t a t i o n o f s p h e r e = r ω = r 2 π n n o w s o l v e$

Physics >> Mechanics part 1 >> Kinematics IIT JEE

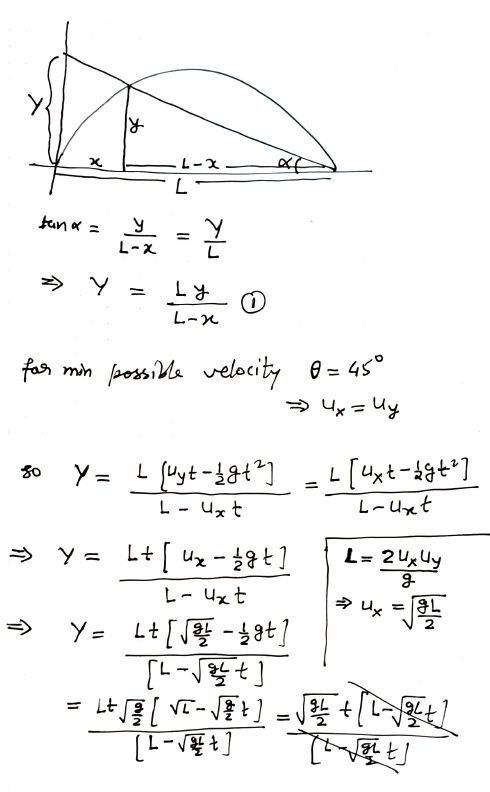
A small ball is thrown from foot of a wall with minimum possible velocity to hit a bulb B on the ground at a distance L away from the wall.Find the expression for height h of shadow of the ball on the wall as a function of time t.Acceleration due to gravity is g.

Asked By: MUDIT

is this question helpfull: 2 0 read solutions ( 1 ) | submit your answer

Joshi sir comment

Physics >> Electricity >> Electric Field and Potential IIT JEE

Asked By: BHASKAR JHA

is this question helpfull: 1 1 submit your answer

Joshi sir comment

$B y v o l u m e c o m p a r i s i o n r a d i u s o f c o m b i n e d d r o p = 2^{1 / 3} r n e t c h a r g e i n t h e n e w d r o p = 2 q n o w p u t t h e s e v a l u e s i n t h e f o r m u l a o f p o t e n t i a l$

Physics >> Mechanics part 1 >> Rotational mechanics IIT JEE

Asked By: AVRANIL SAHA

is this question helpfull: 7 0 submit your answer

Joshi sir comment

$I n f i r s t c a s e F = 2 T = 150 s o T = 75 n e w t o n, N o w i n s e c o n d c a s e s y s t e m i s f r e e t o m o v e a c c e l e r a t i o n o f t h e s y s t e m a = F / 20 f o r 10 k g r o d F - 2 T = 10 a = 10 (F / 20) = F / 2 \Rightarrow F - (F / 2) = 2 T \Rightarrow F = 4 T = 300 n e w t o n$

Physics >> Mechanics part 1 >> Rotational mechanics IIT JEE

what is the moment of inertia of a cube about its diagonal?

Asked By: SHIV GOVIND

is this question helpfull: 1 1 submit your answer

Joshi sir comment

$M o m e n t o f i n e r t i a o f a c u b e a b o u t a l i n e p e r p e n d i c u l a r t o i t s o n e f a c e a n d p a s \sin g t h r o u g h i t s c e n t r e i s m a^{2} / 6 s o a b o u t d i a g o n a l i n e r t i a = l^{2} I_{x} + m^{2} I_{y} + n^{2} I_{z} = (l^{2} + m^{2} + n^{2}) I_{x} (h e r e I_{x} = I_{y} = I_{z}) = I_{x} = m a^{2} / 6 l, m, n a r e d i r e c t i o n \cos i n e s o f t h r e e l i n e s p a s \sin g t h r o u g e c e n t r e o f c u b e a n d p e r p e n d i c u l a r t o e a c h o t h e r$

Physics >> Mechanics part 1 >> Kinematics IIT JEE

While making this paper, I stayed up till late at night working with candle light. I had two

candles of equal length L lit and placed at the same time, as shown in the figure. Immediately

thereafter I noticed that the shadow of the first candle on the left wall is not changing in

length, and the shadow of the second candle on the right wall is being shortened at a speed v.

(Take d1

= 10 cm, d2

= 20 cm, d3

= 30 cm, v = 1 mm/s, L = 20 cm.)

Asked By: AAYUSH MALAVIYA

is this question helpfull: 1 1 submit your answer

Joshi sir comment

Problem is interesting yet not complete. Complete it to get answer

thanks

Physics >> Electricity >> Electric Field and Potential IIT JEE

Initially the spheres a and b are at potential be a and b respectively now sphere b is earthd by closing the switch the poential of a will become

Asked By: ROMEO ROMI

is this question helpfull: 1 3 submit your answer

Joshi sir comment

No meaning can be incurred by this language. Rectify it for getting answer

Physics >> Electricity >> Electric Field and Potential IIT JEE

Asked By: DARIUS

is this question helpfull: 7 0 submit your answer

Joshi sir comment

$S i n c e t h i c k n e s s i s s a m e s o f o r c e p e r u n i t l e n g t h s h o u l d b e s a m e F o r c e p e r u n i t l e n g t h = F / 2 π R C h a r g e d e n s i t y i n t h e s p h e r e i s p r o p o r t i o n a l t o E s o F α q E α σ A E α E^{2} R^{2} T h u s f o r c e p e r u n i t l e n g t h α E^{2} R^{2} / 2 π R α E^{2} R N o w c o m p a r e t h e t w o c a s e s$

Login Here

Registration Form

Your Full Name :

Your Email Address :

Country :

State :

576 - Physics Questions Answers

Login Here

Forget Password

Registration Form