68 - Rotational mechanics Questions Answers

Physics >> Mechanics part 1 >> Rotational mechanics IIT JEE

Asked By: TUSHAR GUPTA

is this question helpfull: 0 0 submit your answer

Physics >> Mechanics part 1 >> Rotational mechanics IIT JEE

Asked By: TUSHAR GUPTA

is this question helpfull: 0 0 submit your answer

Joshi sir comment

Physics >> Mechanics part 1 >> Rotational mechanics IIT JEE

Asked By: TUSHAR GUPTA

is this question helpfull: 0 0 submit your answer

Joshi sir comment

Physics >> Mechanics part 1 >> Rotational mechanics IIT JEE

Please upload solution. Thanks in advance.

Asked By: TUSHAR GUPTA

is this question helpfull: 0 0 submit your answer

Joshi sir comment

Physics >> Mechanics part 1 >> Rotational mechanics IIT JEE

Please post its solution sir, thanks in advance.

Asked By: TUSHAR GUPTA

is this question helpfull: 0 0 submit your answer

Physics >> Mechanics part 1 >> Rotational mechanics IIT JEE

Sir please take this question as a Youtube video. Your explanation is great.

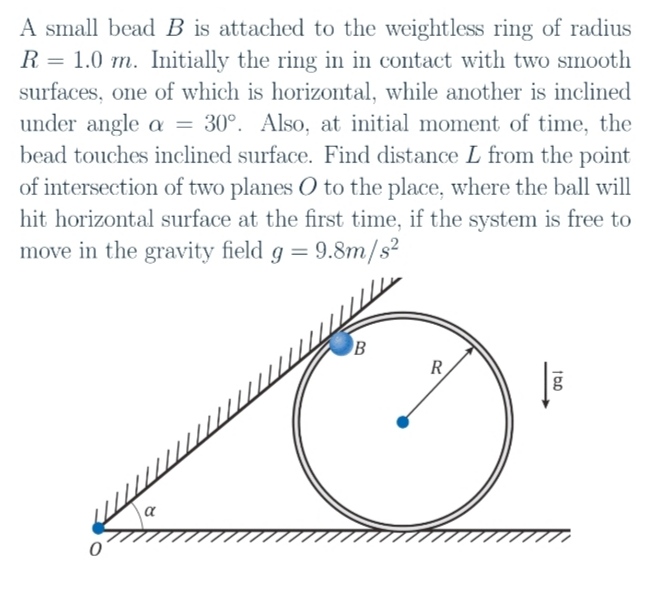
Asked By: AMAN KUMAR

is this question helpfull: 0 1 submit your answer

Joshi sir comment

No horizontal force.

Draw a perpendicular from centre to horizontal plane. Then calculate horizontal distance.

Now solve.

If any problem, then inform

Physics >> Mechanics part 1 >> Rotational mechanics IIT JEE

Asked By: AVRANIL SAHA

is this question helpfull: 7 0 submit your answer

Joshi sir comment

$I n f i r s t c a s e F = 2 T = 150 s o T = 75 n e w t o n, N o w i n s e c o n d c a s e s y s t e m i s f r e e t o m o v e a c c e l e r a t i o n o f t h e s y s t e m a = F / 20 f o r 10 k g r o d F - 2 T = 10 a = 10 (F / 20) = F / 2 \Rightarrow F - (F / 2) = 2 T \Rightarrow F = 4 T = 300 n e w t o n$

Physics >> Mechanics part 1 >> Rotational mechanics IIT JEE

what is the moment of inertia of a cube about its diagonal?

Asked By: SHIV GOVIND

is this question helpfull: 1 1 submit your answer

Joshi sir comment

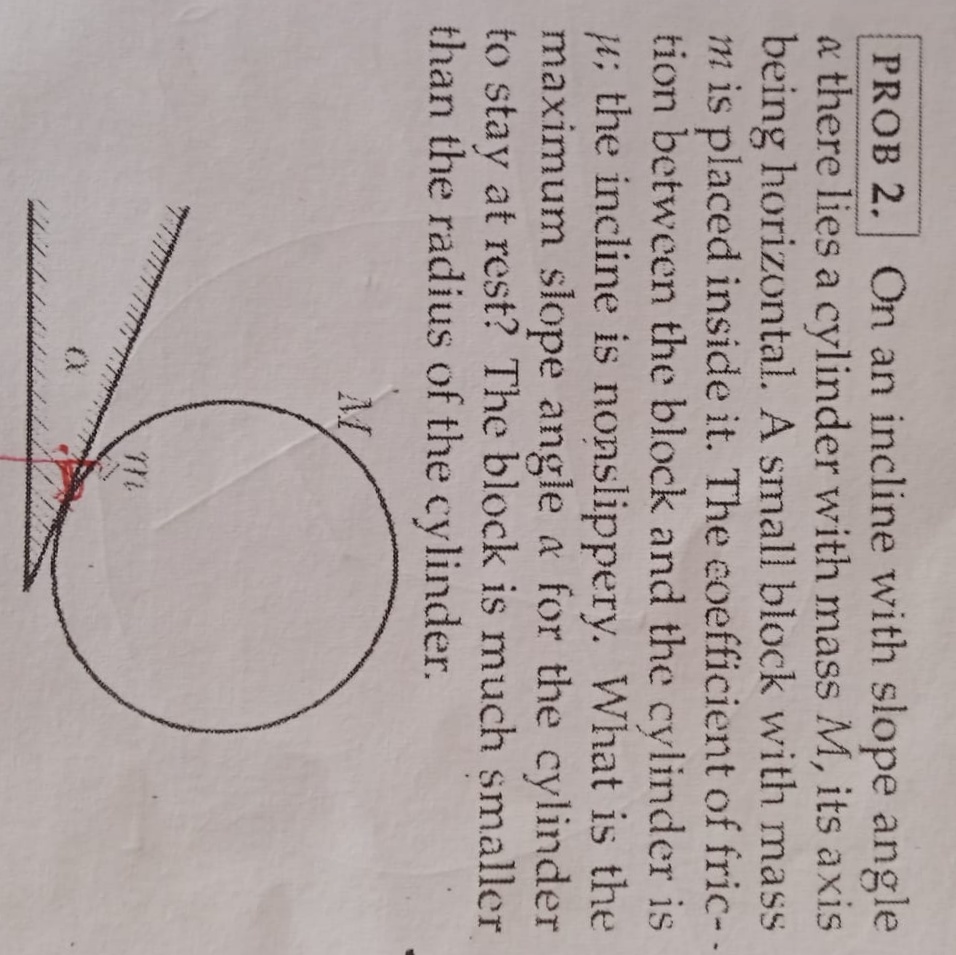
$M o m e n t o f i n e r t i a o f a c u b e a b o u t a l i n e p e r p e n d i c u l a r t o i t s o n e f a c e a n d p a s \sin g t h r o u g h i t s c e n t r e i s m a^{2} / 6 s o a b o u t d i a g o n a l i n e r t i a = l^{2} I_{x} + m^{2} I_{y} + n^{2} I_{z} = (l^{2} + m^{2} + n^{2}) I_{x} (h e r e I_{x} = I_{y} = I_{z}) = I_{x} = m a^{2} / 6 l, m, n a r e d i r e c t i o n \cos i n e s o f t h r e e l i n e s p a s \sin g t h r o u g e c e n t r e o f c u b e a n d p e r p e n d i c u l a r t o e a c h o t h e r$

Physics >> Mechanics part 1 >> Rotational mechanics IIT JEE

Asked By: PRIYANSHU SINGH

is this question helpfull: 2 2 submit your answer

Joshi sir comment

Physics >> Mechanics part 1 >> Rotational mechanics IIT JEE

A rotating ball hits a rough horizontal plane with a vertical velocity $v$ and angular velocity $w$ . Given that the coefficient of friction is $u$ and the vertical component of the velocity after the collision is $v / 2$ , find:

a) the angular velocity after collision;

b) the impulsive ground reaction during the collision

Asked By: UDDESH KUMAR SABAT

is this question helpfull: 1 0 submit your answer

Joshi sir comment

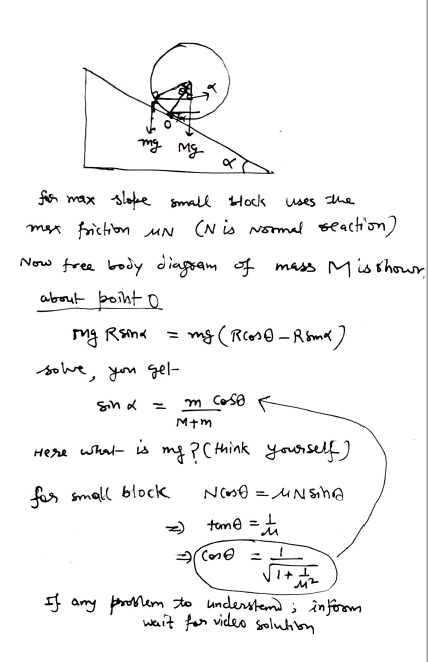
on applying momentum impulse theorem along vertical

-mv+Ndt = mv/2 (1)

by angular momentum angular impulse theorem

$2 m ω r^{2} / 5 - μ N d t r = 2 m ω^{,} r^{2} / 5 (2)$ By eq. (2) get angular velocity.

impulsive ground reaction = $\sqrt{{(N d t)}^{2} + {(μ N d t)}^{2}}$ by using eq. (1), solve it

Login Here

Registration Form

Your Full Name :

Your Email Address :

Country :

State :

68 - Rotational mechanics Questions Answers

Login Here

Forget Password

Registration Form